ALL Algebra Maths Formulas and theorems
Algebra Maths Formulas and theorems
👉(a + b)2 = a2 + b2 + 2ab
👉(a - b)2 = a2 + b2 - 2ab
👉(a2 - b2) = (a + b) (a - b)
👉(a + b)2 + (a - b)2 = 2(a2 + b2)
👉(a + b)2 - (a - b)2 = 4ab
👉(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
👉(a - b + c)2 = a2 + b2 + c2 + 2(-ab - bc + ca)
👉(a + b - c)2 = a2 + b2 + c2 + 2(ab - bc - ca)
👉(a + b)3 = a3 + b3 + 3ab(a + b)
👉(a - b)3 = a3 - b3 - 3ab(a - b)
👉a3 + b3 = (a + b)(a2 - ab + b2)
👉a3 - b3 = (a - b)(a2 + ab + b2)
👉a3 + b3 + c3 - 3abc = (a+b+c)(a2+b2+c2-ab-bc-ca)
If a+b+c = 0, so a3 + b3 + c3 = 3abc
👉(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
👉(a - b)4 = a4 - 4a3b + 6a2b2 - 4ab3 + b4
👉 a4 - b4 = (a - b)(a + b)(a2 + b2)
👉 a5 - b5 = (a - b)(a4 + a3b + a2b2 + ab3 + b4)
👉 a8 - b8 = (a + b)(a - b)(a4 + b4)(a2 + b2)
an - bn = (a - b)(an-1 + an-2b+ ........ + bn-2a + bn-1)
an + bn = (a + b)(an-1 - an-2b + ......... + bn-2a - bn-1)
👉an + bn = (a - b)(an-1 - an-2b+ ........ -bn-2a + bn-1)
👉a-m = 1⁄am
👉1⁄a-m = am
👉(a⁄b)m = am⁄am
👉am⁄an = am-n
👉(an)m = anm
👉a0 = 1
Factor Theorem:
If (x-a) is the factor of f(x)
then f (a) = 0
Remainder Theorem:
If f(x) is divided by (x-a),
then Remainder = f (a)
Some special results
(xn - an)will always be completely divisible by ( x - a).
(xn - an)will always be completely divisible by ( x + a), While n is an even number.
(xn + an)will always be completely divisible by ( x+a), While n is an odd number.
(xn + an)will never be completely divisible by (x-a).
SURDS
 is called Surds of nth Power, while nth
Power of any positive rational number is not equal to ‘a’.
is called Surds of nth Power, while nth
Power of any positive rational number is not equal to ‘a’.Note: It is not necessary to have every irrational number a surd.
Rules of Surds:
Pure Surd:
Mixed Surd:
Polynomial:
p(x) = a0xn + a1xn-1 + a2xn-2 + ........... + an-1x + an
a0, a1 ........... are the positive or negative real number and n is the complete number.
e.g.- 4x3 - 2x2 + 5x - 8
Degree of Polynomial:
The exponent of the term with the largest degree in a polynomial is called the power of that polynomial.
e.g.- x3 + 2x2 + 5x + 8 the term with the largest degree x3, so the polynomial degree is 3.
Linear Polynomial:
If the maximum power of the variable used in the polynomial is 1, it is called a linear polynomial.
e.g.- 4x - 8, 5x, 6x + 4
Quadratic Polynomial:
If the maximum power of the variable used in the polynomial is 2, it is called Quadratic Polynomial.
e.g.- 2x2 + 5x + 8, x2 + 5x - 10

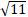



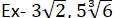

Post a Comment
Please do not enter any site link in the comment box 🚫.