Number System in Hindi

गणित संख्या पद्धति (Number System Math)

Donate me through 👇

UPI ID:- achalup41-1@oksbi

संख्या-प्रणाली (Number system)

गणित के विकास के साथ अनेक संख्या प्रणालियों को विकसित किया गया। प्रत्येक संख्या-प्रणाली में प्रयोग होने वाले अंक, संख्या में भिन्न-भिन्न होते है तथा उनके आधार भी भिन्न-भिन्न होते है। सामान्यतः संख्या प्रणाली का नाम उसमे निहित अंकों की कुल संख्या के आधार पर रखा जाता है। कुछ प्रचलित संख्या प्रणालियाँ निम्न है-

1. बाइनरी संख्या प्रणाली 
2. दशमलव संख्या प्रणाली 
3. ऑक्टल संख्या प्रणाली 
4. हेक्साडेसीमल संख्या प्रणाली 

बाइनरी अंक-प्रणाली (Binary Number System)

बाइनरी अंक प्रणाली में केवल दो अंकों 0 और 1 का ही प्रयोग किया जाता है इसलिए इसके आधार में 2 का प्रयोग करते है 0 या 1 को बिट कहा जाता है। 

1 बाइट (Byte) = 8 बिट्स (Bits)

बाइनरी अंक प्रणाली को 'स्थानीय मान प्रणाली' (Place-Value system) भी कहते है क्योंकि इसमें प्रत्येक बाइनरी अंक का अपना मान होता है जिसे हम 2 की घात के रूप में प्रस्तुत करते है दाई ओर से बाई ओर 2 की घात का मान बड़ता जाता है। 

बाइनरी अंक प्रणाली में बाई ओर जो होते है, पूर्णांक (Integer) को दर्शाते है। बाई ओर की प्रथम बिट सबसे अधिक मान (Largest Weight) की होती है। इसलिए इसे अत्यन्त महत्वपूर्ण अंक (Most Significant Bit, MSB) कहते है। दाई ओर की सबसे अन्तिम बिट का मान सबसे छोटा होता है इसलिए इसे लघुत्तम महत्वपूर्ण अंक (Least Significant Bit, LSB) कहते है। 

उदाहरण 1- (63)₁₀ को बाइनरी संख्या में बदलें। 

हल- 

अतः (63)₁₀ = (111111)₂

उदाहरण 2- (63.125)₁₀ को बाइनरी संख्या में बदलें। 

हल- 

प्रथम चरण- पूर्णांक भाग को सामान्य विधि द्वारा बाइनरी संख्या में परिवर्तित करते है-

(63)₁₀ ⟶ (111111)₂

द्वितीय चरण- भिन्नांक भाग (Fractional part) का बाइनरी परिवर्त्तन निम्न प्रकार से होता है। 

(.125)₁₀ ⟶ (.001)₂

अतः (63.125)₁₀ = (111111.001)₂

दशमलव अंक-प्रणाली (Decimal Number System)

सामान्यतः गणना करने के लिए हम जिस गणना पद्धति का प्रयोग करते है, उसे दशमलव अंक प्रणाली कहते है इस प्रणाली में दस अंकों- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 का प्रयोग होता है। इसे बाई से दाई ओर पढ़ा जाता है दशमलव अंक प्रणाली में अंकों का मान उनके स्थान पर निर्भर करता है। अंकों का मान बाई ओर बढ़ता जाता है क्योंकि इस प्रणाली में अंक के स्थान से उसका मान तय होता है इसलिए इसे 'स्थानीय मान प्रणाली' भी कहते है। उदाहरण के लिए, संख्या 819 में 8 सैकड़ा को, 1 दहाई को व 9 इकाई को दर्शाते है अतः यहाँ 8 अत्यन्त महत्वपूर्ण अंक (MSD) है व 9 लघुतम महत्वपूर्ण अंक (LSD) है। 

बाया ⟶ 819 ← दाया 

उदाहरण 1- (111111)₂ को दशमलव संख्या में बदलें। 

हल- 

= 1 ✕ 2⁵ + 1 ✕ 2⁴ + 1 ✕ 2³ + 1 ✕ 2² + 1 ✕ 2¹ + 1 ✕ 2⁰

= 32 + 16 + 8 + 4 + 2 + 1

= 63

अतः (111111)₂ = (63)₁₀

उदाहरण 2- (111111.101)₂ को दशमलव संख्या में बदलें। 

हल- 

प्रथम चरण- पूर्णांक भाग को सामान्य विधि द्वारा दशमलव संख्या में परिवर्तित करते है-

= 1 ✕ 2⁵ + 1 ✕ 2⁴ + 1 ✕ 2³ + 1 ✕ 2² + 1 ✕ 2¹ + 1 ✕ 2⁰

= 32 + 16 + 8 + 4 + 2 + 1

= 63

(111111)₂ ⟶ (63)₁₀

द्वितीय चरण- भिन्नांक भाग (Fractional part) का दशमलव परिवर्त्तन निम्न प्रकार से होता है इसमें 2 की ऋणात्मक घात से गुणा करके उनको जोड़ते है बाई ओर से दाई ओर चलने पर 2 की ऋणात्मक घात में कमशः वृद्धि होती जाती है  

= 1 ✕ 2^-1 + 0 ✕ 2^-2 + 1 ✕ 2^-3 

= 1 ✕ ¹⁄₂ + 0 ✕ ¹⁄₄ + 1 ✕ ¹⁄₈ 

= 0.5 + 0 + 0.125

= 0.625

(.101)₂ ⟶ (.625)₁₀

अतः (111111.101)₂ = (63.625)₁₀

ऑक्टल अंक प्रणाली (Octal Number System)

ऑक्टल अंक प्रणाली में आठ अंकों 0, 1, 2, 3, 4, 5, 6, 7 का प्रयोग होता है इस अंक प्रणाली का आधार 8 होता है ऑक्टल अंक प्रणाली का एक अंक तीन बाइनरी अंकों के समूह को व्यक्त करता है। ऑक्टल अंक प्रणाली की सारणी निम्न है-

ऑक्टल अंक	बाइनरी संख्या
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

उदाहरण 1- (98)₁₀ को ऑक्टल संख्या में बदलें। 

हल- 

अतः (98)₁₀ = (142)₈

उदाहरण 2- (1101)₂ को ऑक्टल संख्या में बदलें। 

हल- 

(1101)₂ = 1 ✕ 2³ + 1 ✕ 2² + 0 ✕ 2¹ + 1 ✕ 2⁰ 

= 8 + 4 + 0 + 1 = 13

(1101)₂ ⟶ (13)₁₀

अब, (13)₁₀

(13)₁₀ ⟶ (15)₈

अतः (1101)₂ = (15)₈

दूसरी विधि- इसमे 1101 को तीन-तीन बिटो के युग्मों में सयोजित करेंगे। 

001 101 (बाई ओर 0 संख्या का प्रयोग तीन-तीन का युग्म पूरा करने के लिए किया जाता है।)

(1 5)₈   (समतुल्य मान सारणी से रखने पर)

अतः (1101)₂ = (15)₈

उदाहरण 3- (98.95)₁₀ को ऑक्टल संख्या में बदलें। 

हल- 

प्रथम चरण- पूर्णांक भाग को सामान्य विधि द्वारा ऑक्टल संख्या में परिवर्तित करते है-

ऑक्टल संख्या का उदाहरण 1 को देखें। 

(98)₁₀ ⟶ (142)₈

द्वितीय चरण- भिन्नांक भाग (Fractional part) का ऑक्टल संख्या में परिवर्त्तन निम्न प्रकार से होता है-

मुख्यतः यह प्रक्रिया तीन अंकों तक ही दोहराई जाती है। 

(.95)₁₀ ⟶ (.746)₈

अतः (98.95)₁₀ = (142.746)₈

उदाहरण 4- (142.746)₈ को दशमलव संख्या में बदलें। 

हल- 

प्रथम चरण- पूर्णांक भाग को ऑक्टल संख्या से दशमलव संख्या में परिवर्तित निम्न प्रकार से करते है-

= 1 ✕ 8² + 4 ✕ 8¹ + 2 ✕ 8⁰ 

= 64 + 32 + 2 = 98

(142)₈ ⟶ (98)₁₀

द्वितीय चरण- भिन्नांक भाग (Fractional part) का ऑक्टल संख्या से दशमलव संख्या में परिवर्त्तन निम्न प्रकार से होता है-

= 7 ✕ 8^-1 + 4 ✕ 8^-2 + 6 ✕ 8^-3 

= 7 ✕ ¹⁄₈ + 4 ✕ ¹⁄₆₄ + 6 ✕ ¹⁄₅₁₂ 

= 0.875 + 0.0625 + 0.0117

= 0.9492 ≈ 0.95

(.746)₈ ⟶ (.95)₁₀

अतः (142.746)₈  = (98.95)₁₀ 

हेक्साडेसीमल अंक प्रणाली (Hexadecimal Number System)

हेक्साडेसीमल अंक प्रणाली में संख्याओं का आधार 16 होता है। इस प्रणाली की सहायता से सूचनाएं संक्षिप्त रूप में दर्शाई जाती है बड़े कम्प्यूटर्स में आजकल इसी प्रणाली का उपयोग हो रहा है इस प्रणाली में 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F तक 16 अक्षरों का प्रयोग किया जाता है। A, B, C, D, E, F क्रमशः 10, 11, 12, 13, 14, 15 के स्थान पर प्रयोग किया जाता है। यह इस लिए किया जाता है क्योंकि 9 के बाद के समस्त अंक दशमलव प्रणाली के अंतर्गत आते है। 

बाइनरी, ऑक्टल, दशमलव तथा हेक्साडेसीमल अंक प्रणाली में सम्बन्ध सारणी (Relation table among Binary, Octal, Decimal and Hexadecimal Number System)-

सम्बन्ध सारणी निम्न है-

बाइनरी	ऑक्टल	दशमलव	हेक्साडेसीमल
0000	0	0	0
0001	1	1	1
0010	2	2	2
0011	3	3	3
0100	4	4	4
0101	5	5	5
0110	6	6	6
0111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

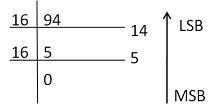
उदाहरण 1- (94.95)₁₀ को हेक्साडेसीमल संख्या में बदलें। 

हल- 

प्रथम चरण- पूर्णांक भाग को हेक्साडेसीमल में परिवर्तित निम्न प्रकार से करते है-

(94)₁₀ ⟶ (5E)₁₆     (14 को E से व्यक्त करते है उपर्युक्त सरणी देखें)

द्वितीय चरण- भिन्नांक भाग (Fractional part) का हेक्साडेसीमल में परिवर्त्तन निम्न प्रकार से होता है-

(.95)₁₀ ⟶ (.F33)₁₆  

अतः (94.95)₁₀  = (5E.F33)₁₆ 

उदाहरण 2- (5E.F33)₁₆ को दशमलव संख्या में बदलें। 

हल- 

प्रथम चरण- पूर्णांक भाग को सामान्य विधि द्वारा दशमलव संख्या में परिवर्तित करते है-

= 5 ✕ 16¹ + E ✕ 16⁰

= 5 ✕ 16¹ + 14 ✕ 16⁰

= 80 + 14 ✕ 1

= 94

(5E)₁₆ ⟶ (94)₁₀

द्वितीय चरण- भिन्नांक भाग (Fractional part) का दशमलव परिवर्त्तन निम्न प्रकार से होता है-

= F ✕ 16^-1 + 3 ✕ 16^-2 + 3 ✕ 16^-3 

= 15 ✕ ¹⁄₁₆ + 3 ✕ ¹⁄₂₅₆ + 3 ✕ ¹⁄₄₀₉₆ 

= 0.9375 + 0.01171 + 0.0007324

= 0.9499  ≈ 0.95

(.F33)₁₆ ⟶ (.95)₁₀

अतः (5E.F33)₁₆ = (94.95)₁₀

संख्याओं के प्रकार (Types of Numbers)

संख्याओं को उनकी प्रकृति और संरचना के आधार पर कई भागों में बाँटा गया है जो निम्न है।

प्राकृत संख्याएँ (Natural numbers)

किसी भी चीज को गिनने के दौरान प्रयोग होने वाली संख्याएँ प्राकृत संख्याएँ होती हैं।  

पाइनोस (Peano's postulates)- "वे संख्याएँ जो वस्तुओं को गिनने के काम आती है।"

इसे 'N' से प्रदर्शित करते है। 

N = {1, 2, 3, 4, 5, ............∞}

पूर्णांक संख्याएँ (Integers)

पूर्णांक -∞ से ∞ तक के समुच्चय को पूर्णांक कहते है इसे 'Z' से प्रदर्शित करते है Z जर्मन वर्ड 'zahlen' के लिए इस्तेमाल किया जाता है जिसका अर्थ 'Numbers' or 'to count' होता है। 

Z = {-∞, ...........-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 .........., ∞}

पूर्णांक संख्याओं को धनात्मक और ऋणात्मक में वर्गीकृत किया जा सकता है धनात्मक पूर्णांक को Z⁺ से और ऋणात्मक पूर्णांक को Z^- से निरूपित किया जाता है 

Z^- = {-∞, ...........-5, -4, -3, -2, -1}

Z⁺ = {1, 2, 3, 4, 5 .........., ∞}

Qus. यदि a और b कोई दो पूर्णांक हो तो, क्या a^b पूर्णांक होंगे?

a^b = 0⁰ (अपरिभाषित)

5^-2 = ¹⁄₂₅ = 0.04

यह सत्य नहीं है क्योकि 0 रखने पर यह अपरिभाषित हो जाता है। 

पूर्ण संख्याएँ (Whole Numbers)

जब प्राकृत संख्याओं में 0 को भी शामिल कर लिया जाता है, तो समुच्चय पूर्ण संख्याओं का समुच्चय बन जाता है इसे 'W' से प्रदर्शित करते है। 

W = {0, 1, 2, 3, 4, 5 .........., ∞}

सम संख्याएँ (Even Numbers)

2 से विभाजित होने वाली प्राकृत संख्याओं को सम संख्या कहते है इसे अधिकतर 'E' से प्रदर्शित करते है। 

E = {2, 4, 6, 8, ............, ∞}

विषम संख्याएँ (Odd Numbers)

वे संख्याएँ जो 2 से पूर्णतः विभाजित नहीं होती है उसे विषम संख्या कहते है इसे 'O' से प्रदर्शित करते है। 

O = { 3, 5, 7, 9 ............, ∞}

भाज्य संख्याएँ या संयुक्त संख्याएँ या यौगिक संख्याएँ (Divisible Number/Composite Number)

वे पूर्ण संख्याएँ जिनके स्वयं और 1 के अतिरिक्त और भी गुणनखण्ड होते है या स्वयं और 1 के अतिरिक्त किसी अन्य संख्या से भी विभाजित होती है उन्हें भाज्य संख्याएँ कहते है। 

जैसे - 4, 6, 8, 9, 10 ............, ∞

'4' के गुणनखण्ड = 1, 2, 4

'9' के गुणनखण्ड = 1, 3, 9

➡ सबसे छोटी भाज्य संख्या '4' है। 

➡ सबसे छोटी विषम भाज्य संख्या '9' है। 

अभाज्य संख्याएँ/रूढ़ संख्याएँ (Prime Number)

वे पूर्ण संख्याएँ जिनके स्वयं और 1 के अतिरिक्त कोई और गुणनखण्ड नहीं होता या स्वयं और 1 के अतिरिक्त किसी अन्य संख्या से विभाजित नहीं होती है उन्हें अभाज्य संख्याएँ कहते है। 

जैसे - 2, 3, 5, 7, 11 ............, ∞

'2' के गुणनखण्ड = 1, 2

'7' के गुणनखण्ड = 1, 7

➡  '2' सबसे छोटी अभाज्य संख्या है और '1' न ही भाज्य संख्या है न अभाज्य संख्या है 

➡ '3' सबसे छोटी विषम अभाज्य संख्या है 

सह-अभाज्य संख्याएँ (Co-Prime Numbers)

दो अभाज्य संख्याएँ जिनमें 1 के अतिरिक्त कोई और उभयनिष्ठ गुणनखण्ड नहीं होता है। 

जैसे - (2, 5), (7, 11), (19, 13), (23, 29)

(7, 11)

7 = 1✕7

11 = 1✕11

1 के अतिरिक्त कोई और उभयनिष्ठ गुणनखण्ड नहीं है।

आपेक्षित अभाज्य संख्या (Relatively prime numbers)

दो संख्याएँ जिनमें 1 के अतिरिक्त कोई और उभयनिष्ठ गुणनखण्ड नहीं होता है दूसरे शब्दों में जिनका HCF, 1 होता है। 

जैसे - (4, 15), (13, 81), (19, 13), (23, 29)

(13, 81)

13 = 1✕13

81 = 1✕3✕3✕3✕3

1 के अतिरिक्त कोई और उभयनिष्ठ गुणनखण्ड नहीं है।

➡ कोई दो क्रमागत संख्याएँ भी सह-अभाज्य संख्याएँ हो सकती है। 

(2, 3), (81, 82), (99, 100) 

➡ कई बार आपेक्षित अभाज्य संख्या को सह-अभाज्य संख्या भी कहते है। 

युग्म अभाज्य संख्या (Twin Prime Number)

वह अभाज्य संख्याएँ जिनके बीच का अंतर '2' हो युग्म अभाज्य संख्याएँ कहते है।

जैसे - (3, 5), (7, 9), (9, 11), (11, 13)

परिमेय संख्याएँ (Rational Number)

ऐसी संख्याएँ जो ^p⁄_q के रूप में निरूपित की जा सकती है उन्हें परिमेय संख्या कहते है जहाँ p व q पूर्णांक हैं, दोनों का कोई उभयनिष्ठ गुणनखण्ड नहीं है और q ≠ 0 है।  

जैसे -²⁄₅, ¹¹⁄₇, ^-5⁄₁₁, ^√25⁄₁, ¹⁄_√36, ²²⁄₇

➡ वे संख्याएँ जिनका दशमलव प्रसार सांत (Terminating Decimals) या समान आवृत्ति (Repeating Decimals) का हो। 

जैसे -  0.6578, 52.67, 0.3333.......= 0.3 , 86.73586586586586.....= 86.73586

दशमलव प्रसार सांत (Terminating Decimals)- वे संख्याएँ जो दशमलव के कुछ अंक बाद रुक जाती है। 

जैसे -  0.6578, 52.6758 

समान आवृत्ति दशमलव (Repeating Decimals)- वे संख्याएँ जिनमें कोई एक संख्या या सख्याओं के समूह की बार-बार पुनरावृत्ति होती है। 

जैसे -  0.33333.....= 0.3, 52.67582582582........= 52.67582

अपरिमेय संख्या (Irrational Numbers)

वे संख्याएँ जिन्हें ^p⁄_q के रूप में नहीं लिखा जा सकता अपरिमेय संख्या कहलाती है। 

जैसे -  √2, √3, √5, √(11), π [क्योंकि π का मान = 3. 4159...... (लगभग)]

➡ वे संख्याएँ जिनका दशमलव प्रसार असांत (Non-Terminating Decimals) व असमान आवृत्ति (Non-repeating Decimals) का होता है अपरिमेय संख्याएँ होती है। 

जैसे -  √2 = 1.41421356........

Qus. 0.33333........को एक परिमेय संख्या (भिन्न संख्या) में बदलें। 

माना x = 0.33333....... ----(i)

प्रश्नानुसार,

x= 0.333333.....

10x = 10✕0.33333.....

10x = 3.3333333.....

10x = 3 + 0.333333.........

10x = 3 + x        [समीकरण '(i)' से]

10x - x = 3

9x = 3

x = ³⁄₉

x = ¹⁄₃

Qus. यदि a और b कोई दो परिमेय संख्या हो, तो निम्नलिखित में से कौन-सी संख्या परिमेय संख्या है?

(i) a+b    (परिमेय संख्या है)

e.g- ¹⁄₃ + ²⁄₅ = ⁽⁵⁺⁶⁾⁄₁₅ = ¹¹⁄₁₅

(ii) a-b    (परिमेय संख्या है)

e.g- ²⁄₃ - ¹⁄₃ = ¹⁄₃

(iii) a✕b    (परिमेय संख्या है)

e.g- ²⁄₃ ✕ ⁴⁄₅ = ⁸⁄₁₅

(iv) ^a⁄_b    (परिमेय संख्या नहीं है)

e.g- ⁽⁰⁾⁄₍₀₎  (अपरिभाषित)

 ^(a)⁄₍₀₎  = ∞ (अपरिभाषित)

(v) a^b    (परिमेय संख्या नहीं है)

e.g- (5)^(1/2) = √5 (अपरिमेय संख्या)

(0)⁰ (अपरिभाषित)

➡ किन्ही दो परिमेय संख्याओं के मध्य अनगिनत परिमेय संख्या होती है। 

➡ किन्ही दो अपरिमेय संख्याओं के मध्य अनगिनत अपरिमेय सख्याओं होती है। 

वास्तविक संख्या (Real Number)

वे परिमेय या अपरिमेय संख्याएँ जिनका वर्ग करने पर एक धनात्मक संख्या प्राप्त हो वास्तविक संख्या कहलाती है। 

जैसे-  -5, -6/7 

(-5)² = 25

 (-6/7)²= 36/49

काल्पनिक संख्या (Imaginary Number) या अवास्तविक संख्या (Non-Real Number)

वे परिमेय या अपरिमेय संख्याएँ जिनका वर्ग करने पर ऋणात्मक संख्या प्राप्त हो काल्पनिक संख्या कहलाती है इसे 'i' से प्रदर्शित करते है जिसे 'iota' कहते है इसका मान √-1 होता है। 

जैसे-  √-5, √(-6/7)

√-5 = √(-1✕5) = i√5

√(-6/7) = √(-1✕6/7) = i√(6/7)

समिश्र संख्या (Complex Number)

समिश्र संख्याएँ काल्पनिक और वास्तविक संख्याओं से मिलकर बनी होती है इन्हे a±ib से निरूपित करते है। 

जहाँ, a = काल्पनिक संख्या 

b = वास्तविक संख्या 

जैसे-  2+i3, 5-i6, -6+i√8

Qus. यदि a और b कोई दो वास्तविक संख्या हो, तो निम्नलिखित में से कौन-सी संख्या वास्तविक संख्या है?

(i) ^a⁄_b (वास्तविक संख्या नहीं है)

e.g.- 5/0 = ∞ 

(ii) a^b (वास्तविक संख्या नहीं है)

e.g.- (-5)^1/2 = √-5 = √(-1✕5) = i√5 (काल्पनिक)

चक्रीय संख्याएँ (Cyclic Numbers)

'n' अंकों की ऐसी संख्या जिसे '1' से लेकर जितने अंकों की वह संख्या है वहां तक किसी भी अंक से गुणा करने पर गुणनफल उन्ही 'n' अंकों की संख्या से बना होता है। इस प्रकार की संख्या को चक्रीय संख्याएँ कहते है।

जैसे-  142857

(संख्या में अंक) n = 6   (1, 2, 3, 4, 5, 6)

1✕142857 = 142857

2✕142857 = 285714

3✕142857 = 428571

4✕142857 = 571428

5✕142857 = 714285

6✕142857 = 857142

पूर्णकालिक संख्या (Perfect Numbers)

वे संख्याऐं जिनके गुणनखण्डों (factors) का योग स्वयं उस संख्या को छोड़कर पुनः वही संख्या आये उस संख्या को पूर्णकालिक संख्या कहते है। 

जैसे-  6, 28, 496

6 के गुणनखण्ड = 1, 2, 3, 6

6 को छोड़कर सभी गुणनखंडो का योग = 1+2+3 = 6

➡ 6 सबसे छोटी पूर्णकालिक संख्या है। 

28 के गुणनखण्ड = 1, 2, 4, 7, 14, 28

28 को छोड़कर सभी गुणनखंडो का योग = 1+2+4+7+14 = 28

496 के गुणनखण्ड = 1, 2, 4, 8, 16, 31, 62, 124, 248, 496

496 को छोड़कर सभी गुणनखंडो का योग = 1+2+4+8+16+31+62+124+248 = 496

➡ यदि कोई संख्या पूर्णकालिक है तो स्वयं सहित इसके सभी गुणनखंडो के व्युत्क्रम का योग हमेशा '2' होगा। 

6 = 1, 2, 3, 6

¹⁄₁ + ¹⁄₂ + ¹⁄₃ + ¹⁄₆ = ^(6+3+2+1)⁄₆ = ¹²⁄₆ = 2

28 = 1, 2, 4, 7, 14, 28

¹⁄₁ + ¹⁄₂ + ¹⁄₄ + ¹⁄₇ + ¹⁄₁₄ + ¹⁄₂₈ = ^{(28+14+7+4+2+1)}⁄₂₈ = ⁵⁶⁄₂₈ = 2

रामानुजन संख्या या हार्डी-रामानुजन संख्या (Ramanujan's number or Ramanujan-Hardy number)

वह संख्या जिसे दो अलग-अलग प्रकार की संख्याओं के घनों के योग  के रूप में लिखा जा है। 

जैसे-  1729 

 हैप्पी संख्या (Happy Number)

किसी संख्या के सभी अंकों के वर्गो का योग करें और यह प्रक्रिया तब तक जारी रखे जब तक कि अंतिम परिणाम '1' न आ जाये पर जिन संख्याओं में अंतिम परिणाम '1' नहीं आता है वह हैप्पी संख्या नहीं है। 

जैसे-  49, 44, 13, 23, 28, 31, 82 

49 = 4² + 9² = 16+81 = 97

97 = 9² + 7² = 81+49 = 130

130 = 1² + 3² + 0² = 1+9+0 = 10

10 = 1² + 0² = 1+0 = 1

और 

28 = 2² + 8² = 4+64 = 68

68 = 6² + 8² = 36+64 = 100

100 = 1² + 0² + 0² = 1+0+0 = 1

पैलिन्ड्रोमिक संख्या (Palindromic Number)

पैलिन्ड्रोमिक संख्या को अंक पैलिन्ड्रोम या संख्यात्मक पैलिन्ड्रोम भी कहते है एक पैलिन्ड्रोमिक संख्या को उल्टा लिखने पर भी संख्या समान ही रहती है दुसरे शब्दों में ऊर्ध्वाधर अक्ष पर परावर्तित समरूपता दिखाई देती है। 

जैसे-  (11)² = 121

(111)² = 12321

(1111)² = 1234321

या 

75257

16561

योग के गुण (Properties of Addition)

संवरक गुण (Closure Property)

दो पूर्णांक संख्याओं का योग सदैव एक पूर्णांक संख्या होगी। 

a+b = c

जहाँ a, b और c पूर्णांक हैं। 

जैसे-  4+5 = 9

3+(-2) = 1

(-4)+3 = -1

क्रमविनिमय गुण (Commutative Property)

इस गुण के अनुसार स्थान बदल देने से संख्या के मान में कोई फर्क नहीं पड़ता है। 

a+b = b+a

जहाँ a, b पूर्णांक हैं। 

जैसे-  4+5 = 9 या 5+4 = 9

(-8)+10 = 2 या 10+(-8) = 2

साहचर्य गुण (Associative Property)

यह तीन या अधिक संख्याओं को जोड़ने के लिए प्रक्रिया प्रदान करता है। 

(a+b)+c = a+(b+c) = a+b+c

जैसे-  (4+3)+5 = 4+(3+5) = 12

योज्य या योगात्मक तत्समक (Additive Identity)

यदि a + 0 = a, अतः शून्य को योगात्मक तत्समक कहते है। 

जैसे-  4+0 = 4

योगात्मक प्रतिलोम (Additive Inverse)

यदि a + (-a) = 0, अतः a और (-a) दोनों एक-दूसरे के योगात्मक प्रतिलोम होंगे। 

जैसे-  4+(-4) = 0, अतः 4 और (-4) दोनों एक-दूसरे के योगात्मक प्रतिलोम है। 

गुणन के गुण (Properties of Multiplication)

संवरक गुण (Closure Property)

दो पूर्णांक संख्याओं का गुणा सदैव एक पूर्णांक संख्या होगी। 

a✕b = c

जहाँ a, b और c पूर्णांक हैं। 

जैसे-  4✕5 = 20 

3✕(-2) = -6

(-4)✕3 = -12

क्रमविनिमय गुण (Commutative Property)

इस गुण के अनुसार स्थान बदल देने से संख्या के मान में कोई फर्क नहीं पड़ता है। 

a✕b = b✕a

जहाँ a, b पूर्णांक हैं। 

जैसे-  4✕5 = 20 या 5✕4 = 20

(-8)✕10 = -80 या 10✕(-8) = -80

साहचर्य गुण (Associative Property)

यह तीन या अधिक संख्याओं को जोड़ने के लिए प्रक्रिया प्रदान करता है। 

(a✕b)✕c = a✕(b✕c) 

जैसे-  (4✕3)✕5 = 4✕(3✕5) = 60

गुणात्मक तत्समक (Multiplicative Identity)

यदि a ✕ 1 = a, अतः 1 को गुणात्मक तत्समक कहते है। 

जैसे-  4✕1  = 4

गुणात्मक प्रतिलोम (Multiplicative Inverse)

यदि a ✕ b = 1, अतः a और b दोनों एक-दूसरे के गुणात्मक प्रतिलोम होंगे। 

या, यदि ^x⁄_y ✕ ^y⁄_x = 1, अतः ^x⁄_y और ^y⁄_x दोनों एक-दूसरे के गुणात्मक प्रतिलोम होंगे। 

जैसे-  4✕¹⁄₄ = 1, अतः 4 और ¹⁄₄ दोनों एक-दूसरे के गुणात्मक प्रतिलोम है। 

या, ³⁄₄✕⁴⁄₃ = 1, अतः ³⁄₄ और ⁴⁄₃ दोनों एक-दूसरे के गुणात्मक प्रतिलोम है।

गुणन का पुनरावृत्त योग (Iterative sum of multiplication)

यदि किसी संख्या का बार-बार योग होता है तो उसका मान उस संख्या और उसकी आवृत्ति के गुणनफल के बराबर होता है। 

a+a+a = 3✕a

जैसे-  4+4+4 = 3✕4 = 12

संख्याओं में भाग संक्रिया (Divison Operation in Numbers)

माना किसी संख्या a को संख्या b से विभक्त करने पर भागफल q तथा शेषफल r है, तब 

a = bq +r,    जहाँ 0 ≤ r < b

a = भाज्य (dividend)

b = भाजक (divisor)

q = भागफल (quotient)

r = शेषफल (remainder)

भाज्य = (भाजक ✕ भागफल) + शेषफल 

➡ (xⁿ - aⁿ) सदैव (x - a) से पूर्णंतया विभक्त होगा, जब n एक विषम संख्या हो। 

➡ (xⁿ + aⁿ) तभी (x + a) से पूर्णंतया विभक्त होगा, जब n एक विषम संख्या हो। 

➡ (xⁿ - aⁿ) तभी (x + a) & (x - a) से पूर्णंतया विभक्त होगा, जब n एक सम संख्या हो। 

➡ (xⁿ + aⁿ) कभी भी (x + a) & (x - a) से पूर्णंतया विभक्त नहीं होगा, जब n एक सम संख्या हो। 

How to find Unit digit in Hindi

Divisibility Rule for 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 in hindi

Number System Questions

Unit digit Questions