HCF and LCM
Free Notes for all types of exams Competition exams like STET, CTET, SSC, Railway, Bank, Lekhpal, NDA, UPSC and other Competition Exams. You get all types of questions (Quantitative Aptitude) with detailed solutions in Hindi/English on this site.
Donate me through 👇
UPI ID:- achalup41-1@oksbi
HCF- Highest Common Factor or GCD- Greatest Common Divisor
LCM- Least Common Multiple or Lowest Common Multiple
Definitions and General Rules
Factor and Multiple
If a number 'a' completely divides another number 'b', then 'a' is called a divisor or a factor of 'b' and 'b' is called a multiple of 'a'.
Example - 5 divides 15 completely, so 5 is called a factor of 15 and 15 is called a multiple of 5.
Let us understand with some more examples-
| factors of 45 | multiples of 5 |
|---|---|
|
45 = 1, 3, 5, 9, 15, 45 45 is, is completely divisible by 1, 3, 5, 9, 15 so 1, 3, 5, 9, 15 are factors of 45 |
5 = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55 All these are multiples of 5, that is, it can be said that the product obtained by multiplying any number by 5 is a multiple of 5. e.g.- 5✕1=5, 5✕2= 10, 5✕3= 15,....5✕9=45 |
Common Factor
A number which completely divides each of two or more numbers is called a common factor. e.g.- 5 numbers will completely divide 10, 20, and 30, so 5 is the common factor of 10, 20, and 30.
HCF (Highest Common Factor)
The biggest number that divides two or more than two numbers is called the HCF of all those numbers e.g.- 10 is the HCF of the numbers 30, 40, 60, 80 because it is the biggest number that can divide all 30, 40, 60, 80.
Common Multiple
The number which is completely divisible by two or more numbers like 60 is completely divisible by 3, 5, 6, 10, 12, 15, so 60 is the common multiple of 3, 5, 6, 10, 12, 15.
LCM (Least Common Multiple)
The smallest number which can be completely divisible by all of two or more numbers is called the least common multiple of all those numbers. e.g.- the L.C.M of 3, 4, 6, 8 is 24 because it is the smallest number that is exactly divisible by all 3, 4, 6, 8.
Methods of Finding the HCF
There are mainly two methods of finding the HCF.
Prime Factorization Method
In prime factors, only those numbers are kept which are either divisible by 1 or themselves
If any two numbers are 35 and 42, then by the method of prime factorization, the HCF is -
Prime factors of 35 = 1, 5, 7
Factors of 42 = 1, 2, 3, 6, 7, 14, 21
Prime factors of 42 = 1, 2, 3, 7
Highest common factor = 7
Hence, the HCF of 35 and 42 is '7'.
Division Method
In this method, the larger number is divided by the smaller one, Divide the divisor again by the remainder. This process continues until the remainder is 0 or, when the remainder is 0, the divisor in that step is called the HCF.
For example, if any two numbers are 35 and 42, then by division method, the HCF is -
Hence, the HCF of 35 and 42 is '7'.
Methods of Finding the LCM
There are mainly two methods of finding the LCM.
Prime Factorization Method
In prime factors, only those numbers are kept which are either divisible by 1 or themselves.
If any of the numbers are 15, 18 and 27, then by the method of prime factorization, the LCM is -
prime factors of 15 = 1, 3, 5
prime factors of 18 = 1, 2, 3, 3
prime factors of 27 = 1, 3, 3, 3
All the prime factors are multiplied to find the least common factor and if any prime factor occurs twice or more, then the one which occurs the most number of times is taken.
= 1✕2✕3✕3✕3✕5 = 270
Hence, the LCM of 15, 18 and 27 is '270'.
Division Method
Let us understand the method of finding the LCM by an example.
LCM of 15, 18 and 27 by the Division method.
= 1✕5✕2✕3✕3✕3 = 270
Relation between Numbers, and LCM, HCF
The formula of HCF and LCM is as follows-
Product of two numbers = HCF✕LCM
Find the HCF and LCM of a fraction
Qus. Find the HCF of 14⁄33, 42⁄55, and 21⁄22 .
Solution- Required HCF = (HCF of 14, 42, 21) ⁄(LCM of 33, 55, 22)
HCF of 14, 42, 21-
prime factors of 14 = 1, 2, 7
prime factors of 42 = 1, 2, 3, 7
prime factors of 21 = 1, 3, 7
HCF of 14, 42, 21 = 7
LCM of 33, 55, 22 -
LCM of 33, 55, 22 = 2✕5✕3✕11 = 330Required HCF = 7 ⁄330
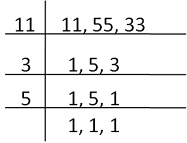
Qus. Find the LCM of 11⁄14, 55⁄42, 33⁄35.
Solution- Required LCM = (LCM of 11, 55, 33) ⁄(HCF of 14, 42, 35)
LCM of 11, 55, 33-
LCM of 11, 55, 33 = 5✕3✕11 = 165
HCF of 14, 42, 35-
prime factors of 14 = 1, 2, 7
prime factors of 42= 1, 2, 3, 7
prime factors of 35 = 1, 3, 5, 7
or
(There is no number which divides 2, 6, 5 So this process will stop here.)
HCF of 14, 42, 21 = 7
Required LCM = 165 ⁄7
Author - Achal Gupta