All trigonometry functions and Identity or formulas list | pdf

Trigonometric function

This is for all competitive exams like SSC, Railway, Bank, TGT, PGT and other competitive exams and academic exams like intermediate or High school exam CBSE, ICSE (class 10, 11, 12) or State board.

UPI ID:- achalup41-1@oksbi

Contact Email ID:- achalup41@gmail.com

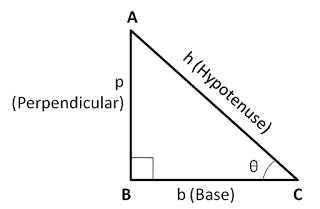
\(sin\hspace{1mm}θ = \frac{p}{h}\)    -1 ≤ sin θ ≤ 1

\(cos\hspace{1mm}θ = \frac{b}{h}\)     -1 ≤ cos θ ≤ 1

\(tan\hspace{1mm}θ = \frac{p}{b}\)     -∞ ≤ tan θ ≤ ∞

\(cot\hspace{1mm}θ = \frac{b}{p}\)     -∞ ≤ cot θ ≤ ∞

\(sec\hspace{1mm}θ = \frac{h}{b}\)     -1 ≥ sec θ ≥ 1

\(cosec\hspace{1mm}θ = \frac{h}{p}\)    -1 ≥ cosec θ ≥ 1

Method Of measuring the angles

1. English System/Degree system

2. French System/Gradian system

3. Circular System/Radian system

1. English System/Degree system

      1 right-angle = 90°

      1° = 60' (60 minute) 

      1' = 60'' (60 second)

2. French System/Gradian system

      1 right-angle = 100^g (100 gradian)

      1^g = 100' (100 minute) 

      1' = 100'' (100 second)

3. Circular System/Radian system

        1 right-angle = 90° = \(\frac{π^C}{2} \left ( \frac{π}{2} \hspace{1mm} Radian \right )\)

\(1^C = \left ( \frac{180\times 7}{22} \right )^{\circ} = 57^{\circ} 16' 22''\)  (approx.)

Relation Between Degree, Gradian and Radian

\[ 90^{\circ} = 100^g = \left ( \frac{π}{2} \right )^C\]

\[\frac{D }{90} = \frac{G}{100} = \frac{2R }{π}\]

π^C = 180°

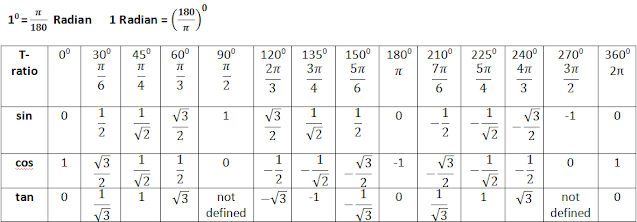
Degree	Radian
30°	\(\frac{\pi}{6}\)
45°	\(\frac{\pi}{4}\)
60°	\(\frac{\pi}{3}\)
90°	\(\frac{\pi}{2}\)
180°	\(\pi\)
270°	\(\frac{3\pi}{2}\)
360°	\(2\pi\)

Trigonometric Identity or formulas

cos (0° - θ) = cos (-θ) = cos θ

sec (0° - θ) = sec (-θ) = sec θ

sin (0° - θ) = sin (-θ) = -sin θ

cosec (0° - θ) = cosec (-θ) = cosec θ

tan (0° - θ) = tan (-θ) = -tan θ

cot (0° - θ) = cot (-θ) = -cot θ

sin \(\frac{A}{2}=\pm \sqrt{\frac{1-cos A}{2}}\)

cos \(\frac{A}{2}=\pm \sqrt{\frac{1+cos A}{2}}\)

tan \(\frac{A}{2}=\pm \sqrt{\frac{1-cos A}{1+cos A}}\)

sin θ cosec θ = 1

cos θ sec θ = 1

tan θ cot θ = 1

sin² θ + cos² θ = 1 

⇒ sin² θ = 1 - cos² θ 

⇒ cos² θ = 1 - sin² θ

sec² θ - tan² θ = 1

⇒ sec θ - tan θ = \(\frac {1}{sec θ + tan θ}\)

cosec² θ - cot² θ = 1

⇒ cosec θ - cot θ = \(\frac {1}{cosec θ + cot θ}\)

sin (A + B) = sin A cos B + cos A sin B

sin (A - B) = sin A cos B - cos A sin B

cos (A + B) = cos A cos B - sin A sin B

cos (A - B) = cos A cos B + sin A sin B

2 sin A cos B = sin (A + B) + sin (A - B)

2 cos A sin B = sin (A + B) - sin (A - B)

2 cos A cos B = cos (A + B) + cos (A - B)

2 sin A sin B = cos (A - B) - cos (A + B)

sin 2θ = 2 sin θ cos θ

sinθ = \(2 sin \frac {θ}{2} cos \frac {θ}{2}\)

sin 2θ = \(\frac {2tanθ}{1 - tan^2 θ}\)

cos 2θ = cos² θ - sin² θ

cos 2θ = 1 - 2sin² θ

cos 2θ = 2cos² θ - 1

cos θ = \(cos^2\frac {θ}{2} - sin^2\frac {θ}{2}\)

cos θ = \(1 - 2sin^2 \frac {θ}{2}\)

cos θ = \(2cos^2 \frac {θ}{2} - 1\)

cos 2θ =\( \frac{1 - tan^2 θ} {1 + tan^2 θ}\)

sin 3θ = 3sin θ - 4sin³ θ

sin θ = \(3 sin \frac {θ}{3} - 4 sin^3 \frac {θ}{3}\)

cos 3θ = 4cos³ θ - 3 cos θ

cos θ = \(4 cos^3 \frac {θ}{3} - 3 cos \frac {θ}{3}\)

sin θ sin 2θ sin 4θ = \(\frac {1}{4}\) sin 3θ cos θ cos 2θ cos 4θ = \(\frac {1}{4}\) cos 3θ tan θ tan 2θ tan 4θ = tan 3θ

tan 3θ  = \(\frac {3tan θ - tan^3θ}{1 - 3tan^2θ}\)

tan θ  = \(\frac {3tan \frac {θ}{3}- tan^3\frac {θ}{3}}{1 - 3tan^2\frac {θ}{3}}\)

sin 3θ = 4 sin (60° - θ) sin θ sin (60° + θ)

cos 3θ = 4 cos (60° - θ) cos θ cos (60° + θ)

tan 3θ = tan (60° - θ) tan θ tan (60° + θ)

3tan 3θ = tan θ + tan (60° + θ) + tan (120° + θ) 

sin (A + B) sin (A - B) = sin² A - sin² B

sin (A + B) sin (A - B) = cos² B - cos² A

sin (A + B + C) = sin A.cos B.cos C + cos A Sin B cos C + Cos A Cos B Sin C - Sin A sin B sin C

cos (A + B) cos (A - B) = cos² A - sin² B

cos (A + B) cos (A - B) = cos² B - sin² A

cos (A + B + C) = cos A cos B cos C - cos A sin B sin C - sin A cos B sin C - sin A sin B cos C

tan (A + B) = \(\frac {tan A + tan B}{1 - tan A tan B}\)

tan (A - B) = \(\frac {tan A - tan B}{1 + tan A tan B}\)

cot (A + B) = \(\frac { cot A cot B - 1}{cot A + cot B}\)

cot (A - B) = \(\frac { cot A cot B + 1}{cot A - cot B}\)

tan \((\frac {A-B}{2} = \sqrt {\frac {1 - cos (A-B)}{1 + cos (A+B)}}\)

tan (A  + B + C) = \(\frac{tan A + tan B +  tan C - tan A.tan B.tan C}{1-tan A.tan B-tan B.tan C-tan C.tanA}\)

If (1 + tan A)(1 + tan B) = 2 then, A + B = 45°

\(\frac {1 + cos θ}{1 - cos θ} = cot^2\frac {θ}{2}\)

\(\frac {1 - cos θ}{1 + cos θ} = tan^2\frac {θ}{2}\)

sin C + sin D = \(2 sin (\frac {C+D}{2}) cos (\frac {C-D}{2})\)

sin C - sin D = \(2 cos (\frac {C+D}{2}) sin (\frac {C-D}{2})\)

cos C + cos D = \(2 cos (\frac {C+D}{2}) cos (\frac {C-D}{2})\)

cos C - cos D = \(2 sin (\frac {C+D}{2}) sin (\frac {D-C}{2})\)

1 + sin 2θ = (sin θ + cos θ)²

1 - sin 2θ = (sin θ - cos θ)²

cot θ + tan θ = 2cosec 2θ

cot θ - tan θ = 2cot 2θ

tan θ.sec 2θ = tan 2θ - tan θ 

tan² θ tan 2θ = tan 2θ - 2tan θ

cos θ cos 2θ cos (2² θ) cos (2³ θ) ..............cos (2ⁿ θ) = \(\frac {sin (2^{n+1}θ)}{2^{n+1}sin θ}\)

cos θ cos 2θ cos (2² θ) cos (2³ θ) ..............cos (2^{n - 1} θ) = \(\frac {sin (2^{n}θ)}{2^{n}sin θ}\)

cos α + cos (α + β) + cos (α + 2β) + ............n terms = \(\frac {sin\hspace{1mm} n\frac{β}{2}}{sin \frac{β}{2}} cos \left (\frac {first \hspace{1mm} angle + last \hspace{1mm} angle}{2}\right )\)

Some Important values

sin 75° = cos 15° = \(\frac {\sqrt{3} + 1}{2\sqrt{2}}\)

cos 75° = sin 15° = \(\frac {\sqrt{3} - 1}{2\sqrt{2}}\)

tan 75° = cot 15° = \(\frac {\sqrt{3} + 1}{\sqrt{3} - 1} = 2 + \sqrt{3}\)

cot 75° = tan 15° = \(\frac {\sqrt{3} - 1}{\sqrt{3} + 1} = 2- \sqrt{3}\)

\(sin 67\tfrac {1°}{2} = cos 22\tfrac {1°}{2} = \frac{1}{2} \sqrt{2+\sqrt{2}}\)

\(cos 67\tfrac {1°}{2} = sin 22\tfrac {1°}{2} = \frac{1}{2} \sqrt{2-\sqrt{2}}\)

\(tan 67\tfrac {1°}{2} = cot 22\tfrac {1°}{2} = \sqrt{2}+1\)

\(cot 67\tfrac {1°}{2} = tan 22\tfrac {1°}{2} = \sqrt{2}-1\)

sin 18° = cos 72° = \(\frac{\sqrt{5}-1}{4}\)

cos 36° = sin 54° = \(\frac{\sqrt{5}+1}{4}\)

cos 18° = sin 72° = \(\frac{\sqrt{10+2\sqrt{5}}}{4}\)

sin 36° = cos 54° = \(\frac{\sqrt{10-2\sqrt{5}}}{4}\)

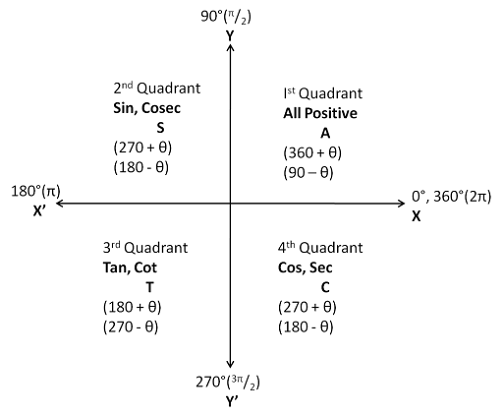
General solution of Trigonometric equations

Trigonometric equation	General solution
sin θ = sin α	θ = nπ + (-1)nα [n ∈ I or n ∈ Z]
cos θ = cos α	θ = 2nπ ± α [n ∈ I or n ∈ Z]
tan θ = tan α	θ = nπ + α [n ∈ I or n ∈ Z]
sin θ = 0 sin θ = sin 0°	θ = nπ [n ∈ I or n ∈ Z]
cos θ = 0 cos θ = cos \(\frac{π}{2}\)	θ = 2nπ ± \(\frac{π}{2}\) or θ = (2n + 1) \(\frac{π}{2}\) or θ = (2n - 1) \(\frac{π}{2}\) [n ∈ I or n ∈ Z]
tan θ = 0 tan θ = tan 0°	θ = nπ [n ∈ I or n ∈ Z]
sin θ = 1 sin θ = sin \(\frac{π}{2}\)	θ = nπ + (-1)n\(\frac{π}{2}\) or θ = (4n + 1)\(\frac{π}{2}\) [n ∈ I or n ∈ Z]
cos θ = 1 cos θ = cos 0°	θ = 2nπ [n ∈ I or n ∈ Z]
tan θ = 1 tan θ = tan \(\frac{π}{4}\)	θ = nπ + \(\frac{π}{4}\) [n ∈ I or n ∈ Z]
sin θ = -1	θ = (4n - 1) \(\frac{π}{2}\) [n ∈ I or n ∈ Z]
cos θ = -1	θ = (2n - 1)π or θ = (2n + 1)π [n ∈ I or n ∈ Z]
tan θ = -1 or tan θ = tan \(\frac{-π}{4}\) or tan θ = tan \(\frac{3π}{4}\)	θ = nπ - \((\frac{-π}{4})\) or θ = nπ + \(\frac{3π}{4}\) [n ∈ I or n ∈ Z]
sin2 θ = sin2 α	θ = nπ ± α [n ∈ I or n ∈ Z]
cos2 θ = cos2 α	θ = nπ ± α [n ∈ I or n ∈ Z]
tan2 θ = tan2 α	θ = nπ ± α [n ∈ I or n ∈ Z]
sin θ = sin α and cos θ = cos α	θ = 2nπ + α [n ∈ I or n ∈ Z]
sin θ = sin α and tan θ = tan α	θ = 2nπ + α [n ∈ I or n ∈ Z]
cos θ = cos α and tan θ = tan α	θ = 2nπ + α [n ∈ I or n ∈ Z]

 Formulas and Properties of Triangle

Half perimeter of the triangle S\( = \frac {a+b+c}{2}\)

Area of triangle △ = \( \frac {1}{2} \times Base \times Height\)

Area of triangle △ = \( \sqrt{S(S-a)(S-b)(S-c)} \)

△ = \(  \frac {1}{2} \times ab \times Sin \hspace{1mm} C \)

△ = \(  \frac {1}{2} \times bc \times Sin \hspace{1mm} A \)

△ = \(  \frac {1}{2} \times ac \times Sin \hspace{1mm} B \)

Where a,b,c are length of triangle sides and A,B,C are angles of triangle.

1. Sine Formula

\( \frac {a}{Sin \hspace{1mm} A} = \frac {b}{Sin \hspace{1mm} B} = \frac {c}{Sin \hspace{1mm} C} \)

\( \frac {Sin \hspace{1mm} A}{a} = \frac {Sin \hspace{1mm} B}{b} = \frac {Sin \hspace{1mm} C}{c} \)

\( \frac {a}{Sin \hspace{1mm} A} = \frac {b}{Sin \hspace{1mm} B} = \frac {c}{Sin \hspace{1mm} C} = K \)

2. Cosine formula

Cos A = \(\frac {b^2+c^2-a^2}{2bc}\)

Cos B = \(\frac {a^2+c^2-b^2}{2ac}\)

Cos C = \(\frac {a^2+b^2-c^2}{2ab}\)

3. Projection formula

a = b cos C + c cos B

b = a cos C + c cos A

c = a cos B + b cos A

4. Tangent formula (Napier's formula)

\(tan \left ( \frac {A-B}{2} \right ) = \left ( \frac {a-b}{a+b} \right ) cot \frac {C}{2} \)

\(tan \left ( \frac {B-C}{2} \right ) = \left ( \frac {b-c}{b+c} \right ) cot \frac {A}{2} \)

\(tan \left ( \frac {C-A}{2} \right ) = \left ( \frac {c-a}{c+a} \right ) cot \frac {B}{2} \)

5. Half angle formula

sin \( \frac {A}{2} = \sqrt {\frac {(S-b)(S-c)}{bc}} \)

sin \( \frac {B}{2} = \sqrt {\frac {(S-a)(S-c)}{ac}} \)

sin \( \frac {C}{2} = \sqrt {\frac {(S-a)(S-b)}{ab}} \)

cos \( \frac {A}{2} = \sqrt {\frac {S(S-a)}{bc}} \)

cos \( \frac {B}{2} = \sqrt {\frac {S(S-b)}{ac}} \)

cos \( \frac {C}{2} = \sqrt {\frac {S(S-c)}{ab}} \)

tan \( \frac {A}{2} = \sqrt {\frac {(S-b)(S-c)}{S(S-a)}} \)

tan \( \frac {B}{2} = \sqrt {\frac {(S-a)(S-c)}{S(S-b)}} \)

tan \( \frac {C}{2} = \sqrt {\frac {(S-a)(S-b)}{S(S-c)}} \)

tan \( \frac {A}{2} = \sqrt {\frac {△}{S(S-a)}} \)

tan \( \frac {B}{2} = \sqrt {\frac {△}{S(S-b)}} \)

tan \( \frac {C}{2} = \sqrt {\frac {△}{S(S-c)}} \)

Some other important formula in triangle

In-radius (r) = \( \frac {△}{S} \)

Circum radius (R) = \( \frac {abc}{4△} \)

\( \frac {a}{Sin \hspace{1mm} A} = \frac {b}{Sin \hspace{1mm} B} = \frac {c}{Sin \hspace{1mm} C} = 2R \)

\( \frac {a}{Sin \hspace{1mm} A} = \frac {b}{Sin \hspace{1mm} B} = \frac {c}{Sin \hspace{1mm} C} = \frac {abc}{2△} \)

r = (S - a) tan \(\frac {A}{2}\)

r = (S - a) tan \(\frac {B}{2}\)

r = (S - a) tan \(\frac {C}{2}\)

ex-radius r₁ = \( \frac {△}{S-a} \)

ex-radius r₂ = \( \frac {△}{S-b} \)

ex-radius r₃ = \( \frac {△}{S-c} \)

In Triangle ABC :-

sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C

cos 2A + cos 2B + cos 2C = -1 - 4 cos A cos B cos C

sin A + sin B + sin C = 4 cos \(\frac {A}{2}\) cos \(\frac {B}{2}\) cos \(\frac {C}{2}\)

cos A + cos B + cos C = 1 + 4 sin \(\frac {A}{2}\) sin \(\frac {B}{2}\) sin \(\frac {C}{2}\)

sin² A + sin² B + sin² C = 2 + 2 cos A cos B cos C

cos² A + cos² B + cos² C = 1 - 2 cos A cos B cos C

tan A + tan B + tan C = tan A tan B tan C

cot A cot B + cot B cot C + cot C cot A = 1

Trigonometric functions series or progressions 

This series is also called Taylor's expansions. 

sin x = \(x - \frac {x^3}{3!} + \frac {x^5}{5!} - \frac {x^7}{7!} + .......\)

cos x = \(1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + ......\)

\(tan x = x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17x^7}{315} + \frac{62x^9}{2835} +......+\frac {2^{2n}(2^{2n} - 1)B_nx^{2n-1}}{(2n)!}+ .....\)

B_n = Bernoulli Number

\(cosec x = \frac{1}{x} + \frac{x}{6} + \frac{7x^3}{360} + \frac{31x^5}{15120} +......+\frac {2(2^{2n} - 1)B_nx^{2n-1}}{(2n)!}+ .....\)

sec x = \(1 + \frac{x^2}{2} + \frac{5x^4}{24} + \frac{61x^6}{720} + ...... + \frac{E_nx^{2n}}{(2n)!} + ....\)

E_n = Euler Number

cot x = \(\frac{1}{x} - \frac{x}{3} - \frac{x^3}{45} - \frac{2x^5}{945} -......-\frac {2^{2n}B_nx^{2n-1}}{(2n)!}+ .....\)

If you need any formula for trigonometry. you can tell it in the comment box. I will soon provide it.

Download pdf

Don't forget to share with friends and support🙏