Geometry, properties, mensuration formula 3D

 Three-dimensional shapes (Solid shapes)

Three-dimensional shapes have length, width and height. Three-dimensional shapes can only be defined in a 3D Co-ordinate geometry. The properties and formulas of all three-dimensional shapes in mathematics are given below.

Cube

The cube is made up of 6 squares. its length, width and height are equal.

Properties-

Surface- 6

Edges- 12

Vertices- 8

Formulas-

Total surface area = 6(side)²

Lateral surface area = 4(side)²

Volume = (side)³

Diagonal = \(side\sqrt {3}\)

Cuboid

It is made up of 6 rectangles. its length, width and height are different. 

Properties-

Surface- 6

Edges- 12

Vertices- 8

Formulas-

Total surface area = 2(L✕W + W✕H + H✕L)

Lateral surface area = 2(W✕H + H✕L)

Volume = Leight✕Width(breath)✕Height =L✕W✕H

Diagonal = \(\sqrt {L^2 + W^2 + H^2}\)

Euler's Formula

Euler's Formula for polyhedral figures like cubes and cuboids.

V + F - E = 2

F- Surfaces/Faces

E- Edges

V- Vertices

Cylinder 

The top and bottom surfaces of the cylinder are circular and the side is covered with a curved surface.

Formulas-

Curved surface area = 2πrh

Total surface area  = 2πrh + πr² + πr² = 2πr(h + r)

Volume = πr²h

r ⟶ Radius of the cylinder

h ⟶ Height of cylinder

Hollow cylinder

The hollow cylinder's top and bottom surfaces are ring surfaces with two curved surfaces. Outer curved surface and inner-curved surface.

Formulas-

Curved surface area = 2πRh + 2πrh = 2πrh(R + r)

Total surface area  = 2πrh(R + r) + 2(πR² - πr²) =  2π(R + r) (h + R - r)

Volume = πR²h - πr²h = πh(R² - r²)

R ⟶ Radius of the outer cylinder

r ⟶ Radius of the inner cylinder

h ⟶ Height of cylinder

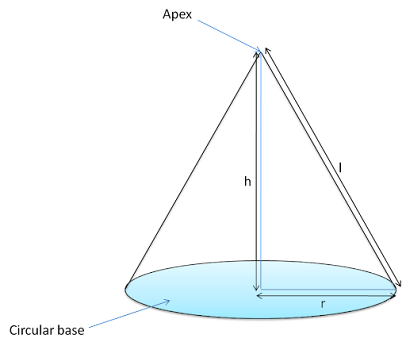
Cone

Cone has a flat circular base and a pointed top. The pointed top of the cone is called the 'Apex' and the side is covered with a curved surface.

Formulas-

Curved surface area = \(\frac {1}{2} ✕ perimeter \space of \space base ✕ slant \space height \) 

         = \(\frac {1}{2} ✕ 2πr ✕ l \) = πrl

Total surface area  = πrl + πr² =  πr(l + r)

Volume = \(\frac {1}{3} ✕ πr^2h \)

l = \( \sqrt {r^2 + h^2} \)

h ⟶ Height of the cone

r ⟶ Radius of the cone 

l ⟶ Slant height of the cone 

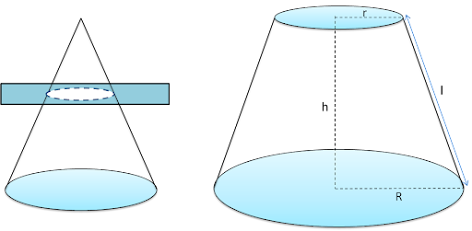
Frustum

If we cut off the top end of the cone, we get a frustum.

Formulas-

Curved surface area = πrl + πRl

Total surface area  = πl (r + R) + πr² + πR² =  πl(r + R) + π(r² + R²)

Volume = \(\frac {πh}{3} ✕ (r^2 + R^2 + Rr) \)

l = \( \sqrt {(R - r)^2 + h^2} \)

h ⟶ Height of the cone

R ⟶ Radius of the base

r ⟶ Radius of the top

l ⟶ Slant height of the frustum

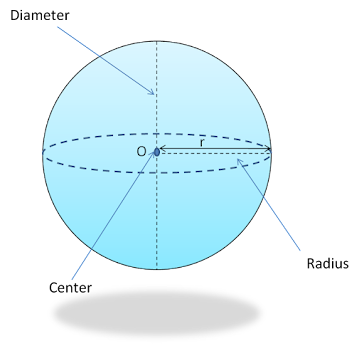
Sphere

The sphere has no vertex or edge. It looks similar from all sides just like a ball.

Formulas-

Curved surface area or Total surface area = 4πr²

Volume = \(\frac {4}{3} ✕ πr^3 \)

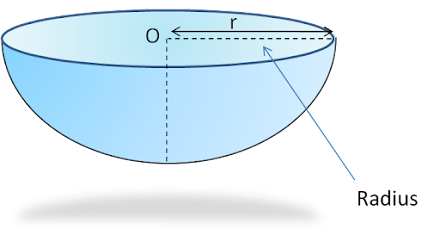
Semisphere

If the sphere is cut from the middle, then a semisphere is obtained.

Formulas-

Curved surface area = 2πr²

Total surface area  = 2πr² + πr² = 3πr²

Volume = \(\frac {2}{3} ✕ πr^3 \)

Prism

The prism consists of identical polygons at the top and bottom. 

Formulas-

Lateral surface area = Perimeter of base ✕ Height

Total surface area  = Perimeter of base ✕ Height + 2✕area of the triangle

Volume = Area of base ✕ height

Pyramid

It has a square at its base but has triangles of equal size on all four sides.

Lateral surface area = \( \frac {1}{2}✕Perimeter \space of \space base ✕ slant \space Height \)

Total surface area  = \( \frac {1}{2}✕Perimeter \space of \space base ✕ slant \space Height + area \space of \space base \)

Volume = \( \frac {1}{3}✕area \space of \space base ✕ Height \)

l = \( \sqrt {h^2 + a^2} \)

h ⟶ Height of the pyramid

l ⟶ Slant height of the pyramid

Tetrahedron

Its four faces are of the same triangle(equilateral triangle) shape.

Lateral surface area = \( \frac {3}{4}✕\sqrt {3} (side)^2 \)

Total surface area  = \( \sqrt {3} (side)^2 \)

Volume = \( \frac {\sqrt 2}{12}✕(side)^3 \)