Simplification Questions with solution

June 01, 2022 June 12, 2022

It is for all Competition exams Free mock test (Practice set)/quiz/MCQ is for all types of exams like STET, CTET, SSC, Railway, Bank, SBI and Bank PO, Clerk, Lekhpal, NDA, UPSC and other Competition Exams. You get all types of questions (Quantitative Aptitude) with detailed solutions in Hindi/English on this site.

Donate me through 👇

UPI ID:- achalup41-1@oksbi

1. Simplify||सरलीकरण कीजिए \(\frac{1}{3+\frac{1}{2-\frac{1}{\frac{7}{9}}}}+\frac{17}{22}\)

1. \(\frac{12}{22}\)

2. \(\frac{22}{5}\)

3. \(\frac{5}{22}\)

4. 1

... Answer is 4)
= \(\frac{1}{3+\frac{1}{2-\frac{9}{7}}}+\frac{17}{22}\)
= \(\frac{1}{3+\frac{1}{\frac{14-9}{7}}}+\frac{17}{22}\)
= \(\frac{1}{3+\frac{7}{5}}+\frac{17}{22}\)
= \(\frac{1}{\frac{15+7}{5}}+\frac{17}{22}\)
= \(\frac{5}{22}+\frac{17}{22}\)
= \(\frac{22}{22}\)
= 1

2. If \(x = 1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{2}}}}\), then \(2x+\frac{7}{4}\) =?

यदि \(x = 1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{2}}}}\) हो, तो \(2x+\frac{7}{4}\) = ?

1. 3

2. 4

3. 5

4. 6

... Answer is 3)
\(x = 1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{2}}}}\)
= \(1+\frac{1}{1+\frac{1}{1+\frac{1}{\frac{3}{2}}}}\)
= \(1+\frac{1}{1+\frac{1}{1+\frac{2}{3}}}\)
= \(1+\frac{1}{1+\frac{1}{\frac{3+2}{3}}}\)
= \(1+\frac{1}{1+\frac{3}{5}}\)
= \(1+\frac{1}{\frac{5+3}{5}}\)
= \(1+\frac{5}{8}\)
= \(\frac{13}{8}\)
∴\(2x+\frac{7}{4}\)
= \(2✕\frac{13}{8}+\frac{7}{4}\)
= \(\frac{13}{4}+\frac{7}{4}\)
= \(\frac{20}{4}\)
= 5

3. Simplify||सरलीकरण कीजिए \(\sqrt{\frac{4\tfrac{1}{7}-2\tfrac{1}{4}}{3\tfrac{1}{2}+1\tfrac{1}{7}}\div \frac{2}{2+\frac{1}{2+\frac{1}{5-\frac{1}{5}}}}}\)

1. 1

2. 4

3. 3

4. 2

... Answer is 1)
\(\sqrt{\frac{4\tfrac{1}{7}-2\tfrac{1}{4}}{3\tfrac{1}{2}+1\tfrac{1}{7}}\div \frac{2}{2+\frac{1}{2+\frac{1}{5-\frac{1}{5}}}}}\)
= \(\sqrt{\frac{\frac{29}{7}-\frac{9}{4}}{\frac{7}{2}+\frac{8}{7}}\div \frac{2}{2+\frac{1}{2+\frac{1}{\frac{25-1}{5}}}}}\)
= \(\sqrt{\frac{\frac{116-63}{28}}{\frac{49+16}{14}}\div \frac{2}{2+\frac{1}{2+\frac{5}{24}}}}\)
= \(\sqrt{\frac{53}{28}\times\frac{14}{65}\div \frac{2}{2+\frac{1}{\frac{48+5}{24}}}}\)
= \(\sqrt{\frac{53}{130}\div \frac{2}{2+\frac{24}{53}}}\)
= \(\sqrt{\frac{53}{130}\div \frac{2}{\frac{106+24}{53}}}\)
= \(\sqrt{\frac{53}{130}\div \frac{53}{130}}\)
= \(\sqrt{\frac{53}{130}\times \frac{130}{53}}\)
= \(\sqrt{1}\)
= 1

4. \(\frac{\frac{1}{4}\times \frac{3}{4}\div 1\tfrac{1}{4}of\frac{2}{5}+\frac{1}{8}}{\frac{2}{5}\div 1\tfrac{2}{3}of\frac{3}{25}+1\tfrac{2}{3}of\frac{3}{25}+1\tfrac{3}{4}-\frac{1}{2}}\div \frac{\frac{1}{3}-\frac{1}{3}of\frac{3}{5}}{\frac{1}{5}-\frac{1}{5}of\frac{5}{7}}\)

1. \(\frac{3}{4}\)

2. \(\frac{6}{91}\)

3. \(\frac{31}{4}\)

4. 1

... Answer is 2)
V - Vinculum
B - Bracket
O - Of
D - Division
M - Multiplication
A - Addition
S - Subtraction
= \(\frac{\frac{1}{4}\times \frac{3}{4}\div \frac{5}{4}of\frac{2}{5}+\frac{1}{8}}{\frac{2}{5}\div \frac{5}{3}of\frac{3}{25}+\frac{5}{3}of\frac{3}{25}+\frac{7}{4}-\frac{1}{2}}\div \frac{\frac{1}{3}-\frac{1}{3}of\frac{3}{5}}{\frac{1}{5}-\frac{1}{5}of\frac{5}{7}}\)
= \(\frac{\frac{1}{4}\times \frac{3}{4}\div \frac{1}{2}+\frac{1}{8}}{\frac{2}{5}\div \frac{1}{5}+\frac{7}{4}-\frac{1}{2}}\div \frac{\frac{1}{3}-\frac{1}{5}}{\frac{1}{5}-\frac{1}{7}}\)
= \(\frac{\frac{1}{4}\times \frac{3}{4}\times \frac{2}{1}+\frac{1}{8}}{\frac{2}{5}\times \frac{5}{1}+\frac{7}{4}-\frac{1}{2}}\div \frac{\frac{5-3}{15}}{\frac{7-5}{35}}\)
= \(\frac{\frac{3}{8}+\frac{1}{8}}{2+\frac{7}{4}-\frac{1}{2}}\div \frac{\frac{2}{15}}{\frac{2}{35}}\)
= \(\frac{\frac{3}{8}+\frac{1}{8}}{2+\frac{7}{4}-\frac{1}{2}}\div \left ( \frac{2}{15}\times\frac{35}{2} \right )\)
= \(\frac{\frac{4}{8}}{2+\frac{7-2}{4}}\div \left ( \frac{7}{3} \right )\)
= \(\frac{\frac{4}{8}}{\frac{13}{4}}\times \left ( \frac{3}{7} \right )\)
= \(\frac{1}{2}\times\frac{4}{13}\times \frac{3}{7} \)
= \(\frac{2}{13}\times \frac{3}{7} \)
= \(\frac{6}{91}\)

5. Find the value of \(\frac{1}{5}+999\tfrac{494}{495}\times 99\)

\(\frac{1}{5}+999\tfrac{494}{495}\times 99\) का मान ज्ञात कीजिए।

1. 90000

2. 99000

3. 90900

4. 99990

... Answer is 2)
\(\frac{1}{5}+999\tfrac{494}{495}\times 99\)
= \(\frac{1}{5}+\frac{999\times 495 + 494}{495}\times 99\)
= \(\frac{1}{5}+\frac{999\times 495 + 494}{5}\)
= \(\frac{1 + (1000-1)\times 495 + 494}{5}\)
= \(\frac{1 + 495000 - 495 + 494}{5}\)
= \(\frac{1 + 495000 - 1}{5}\)
= \(\frac{495000}{5}\)
= 99000

6. Simplify||सरलीकरण कीजिए \(8.7-\left [ 7.6-\left\{6.5 -\left ( 5.4-\overline{4.3-2} \right )\right\} \right ]\)

1. 2.5

2. 3.5

3. 4.5

4. 5.5

... Answer is 3)
\(8.7-\left [ 7.6-\left\{6.5 -\left ( 5.4-\overline{4.3-2} \right )\right\} \right ]\)
= \(8.7-\left [ 7.6-\left\{6.5 -\left ( 5.4-2.3 \right )\right\} \right ]\)
= \(8.7-\left [ 7.6-\left\{6.5 -3.1\right\} \right ]\)
= \(8.7-\left [ 7.6-3.4 \right ]\)
= \(8.7-4.2\)
= 4.5

7. Simplify||सरलीकरण कीजिए \(\frac{0.05\times0.05\times0.05-0.04\times0.04\times0.04}{0.05\times0.05+0.002+0.04\times0.04}\)

1. 1

2. 0.1

3. 0.01

4. 0.001

... Answer is 3)
\(\frac{0.05\times0.05\times0.05-0.04\times0.04\times0.04}{0.05\times0.05+0.002+0.04\times0.04}\)
∵ a³ - b³ = (a - b)(a² + ab + b²)
= \(\frac{0.05^{3}-0.04^{3}}{0.05^{2}+0.002+0.04^{2}}\)
= \(\frac{\left ( 0.05 - 0.04 \right )\left ( 0.05^{2}+0.05\times0.04+0.04^{2} \right )}{0.05^{2}+0.002+0.04^{2}}\)
= 0.05 - 0.04
= 0.01

8. If '+' means '÷', '✕' means '-', '÷' means '✕' and '-' means '+', then what will be the value of the following expression?

यदि '+' का अर्थ है '÷', '✕' का अर्थ है '-', '÷' का अर्थ है '✕' और '-' का अर्थ है '+' तो निम्नलिखित व्यंजक का मान क्या होगा?

9 + 3 ÷ 4 - 8 ✕ 2 = ?

1. \(6\tfrac{1}{4}\)

2. \(6\tfrac{3}{4}\)

3. \(-1\tfrac{3}{4}\)

4. 18

... Answer is 4)
= 9 + 3 ÷ 4 - 8 ✕ 2
= 9 ÷ 3 ✕ 4 + 8 - 2
= \(= \frac{9}{3}\times 4+8-2\)
= 3 ✕ 4+6
= 18

9. Simplify||सरलीकरण कीजिए

\(\left ( 113^{2}+115^{2}+117^{2}-113\times 115-115\times 117-117\times 113 \right)\)

1. 0

2. 4

3. 8

4. 12

... Answer is 4)
\(a^{2}+b^{2}+c^{2}-ab-bc-ac\)
\(= \frac{1}{2}\left ( 2a^{2}+2b^{2}+2c^{2}-2ab-2bc-2ac \right )\)
∵\(= \frac{1}{2}\left [ (a-b)^{2}+(b-c)^{2}+(c-a)^{2} \right ]\)
\(= \frac{1}{2}\left [ (113-115)^{2}+(115-117)^{2}+(117-113)^{2} \right ]\)
where|जहाँ a = 113, b = 115, c = 117
\(= \frac{1}{2}\left [ (-2)^{2}+(-2)^{2}+(4)^{2} \right ]\)
\(= \frac{1}{2}\left ( 4+4+16 \right )\)
\(= \frac{1}{2}\left ( 24 \right )\)
= 12

10.

\(\left ( 999\tfrac{1}{7}+999\tfrac{2}{7}+999\tfrac{3}{7}+999\tfrac{4}{7}+999\tfrac{5}{7}+999\tfrac{6}{7} \right )=?\)

1. 2997

2. 5979

3. 5997

4. 5994

... Answer is 3)

∵=\( \left ( 6\times999 \right )+\frac{1}{7}+\frac{2}{7}+\frac{3}{7}+\frac{4}{7}+\frac{5}{7}+\frac{6}{7} \)
\(= 6\times \left ( 1000-1 \right )+\frac{21}{7}\)
= (6000-6+3)
= 5997

11. \(\frac{0.342\times 0.684}{0.000342\times 0.000171}\) का वर्गमूल है-

\(\frac{0.342\times 0.684}{0.000342\times 0.000171}\) is the square root of-

1. 250

2. 2500

3. 2000

4. 4000

... Answer is 3)
= \(\frac{0.342\times 0.684}{0.000342\times 0.000171}\)
= \(\frac{342\times 684\times 1000000}{342\times 171}\)
= \(\frac{684\times 1000000}{171}\)
= 4✕1000000
square root|वर्गमूल = \(\sqrt{4\times 1000000}\)
= 2000

12. If the expression \(\frac{x^{2}}{y^{2}}+tx+\frac{y^{2}}{4}\) is a perfect square, then what will be the value of t?

यदि व्यंजक \(\frac{x^{2}}{y^{2}}+tx+\frac{y^{2}}{4}\) एक पूर्ण वर्ग हो, तो t का मान कितना होगा?

1. ±1

2. ±2

3. 0

4. ±3

... Answer is 1)
= If|यदि \(a=\frac{x}{y}, b=\frac{y}{2}\)
= So|तो,\(\frac{342\times 684\times 1000000}{342\times 171}\)
= \(\pm2ab=\pm 2\times \frac{x}{y}\times \frac{y}{2}\)
= ±x
∴tx = ±x
t = ±1

13. If (x + 7954✕7956) is a square number, then what will be the value of 'x'?

यदि (x + 7954✕7956) एक वर्ग संख्या हो तो 'x' का मान क्या होगा?

1. 1

2. 16

3. 9

4. 4

... Answer is 1)
= (x + 7954✕7956)
= x + 7954✕(7954 + 2)
= (7954)² + 2✕7954✕1 + x
For the above to be a whole number|उपर्युक्त को पूर्ण संख्या होने के लिए,
x = 1² = 1

14. The smallest number which when added to 680621 makes the sum a perfect square number?

वह सबसे छोटी संख्या, जिसे 680621 में जोड़ने पर योगफल एक पूर्ण वर्ग संख्या बन जाए?

1. 4

2. 5

3. 6

4. 8

... Answer is 1)

∴(824)² < 680621 < (825)²
= (825)² - 680621
= 680625 - 680621
= 4
Short trick
भाजक + 1 - शेषफल | divisor + 1 - remainder
= 1648+1 - 1645
= 1649 - 1645
= 4

15. For the number 1276* to be a perfect square, the value of the missing digit (*) will be?

संख्या 1276* को एक पूर्ण वर्ग संख्या होने के लिए, लुप्त अंक (*) का मान होगा?

1. 1

2. 4

3. 8

4. 9

... Answer is 4)

Obviously 9 will come in place of *.|स्पष्टतः * के स्थान पर 9 आएगा।

16. What is the smallest number subtracted from 4750 to get a perfect square number?

4750 में से किस सबसे छोटी संख्या को घटाने पर एक पूर्ण वर्ग संख्या प्राप्त होगी?

1. 126

2. 162

3. 216

4. 612

... Answer is 1)

So on subtracting 126, the remaining number will become a perfect square of 68.|अतः 126 घटाने पर शेष संख्या 68 का पूर्ण वर्ग बन जाएगा।

17. What is the least positive integer to be subtracted from 3011 ✕ 3012 so that the remainder is a perfect square?

3011 ✕ 3012 से कौन सा न्यूनतम धन पूर्णांक घटाया जाए कि शेषफल पूर्ण वर्ग हो?

1. 3009

2. 3010

3. 3011

4. 3012

... Answer is 3)
3011 ✕ 3012
= 3011 ✕ (3011 + 1)
= (3011)² + 3011
Obviously subtracting 3011 will make the number a perfect square.|स्पष्टतः 3011 घटाने पर संख्या पूर्ण वर्ग बन जाएगी।

18. By what smallest number should 5808 be multiplied so that it becomes a perfect square?

5808 को किस छोटी से छोटी संख्या से गुणा किया जाए कि वह पूर्ण वर्ग बन जाए?

1. 2

2. 7

3. 11

4. 3

... Answer is 4)

= 2 ✕ 2 ✕ 2 ✕ 2 ✕ 3 ✕ 11 ✕ 11
Obviously multiplying by 3 will make the number a perfect square.|स्पष्टतः 3 से गुणा करने पर संख्या पूर्ण वर्ग बन जाएगी।

19. What is the least number by which 20184 will be divided to get a perfect square?

वह छोटी से छोटी संख्या जिससे 20184 को भाग देने पर एक पूर्ण वर्ग प्राप्त होगा?

1. 2

2. 3

3. 5

4. 6

... Answer is 4)

∴20184 = 2 ✕ 2 ✕ 2 ✕ 3 ✕ 29 ✕ 29
= 2² ✕ 2 ✕ 3 ✕ 29²
= 2² ✕ 6 ✕ 29²
Obviously dividing by 6 will make the number a perfect square.|स्पष्टतः 6 से भाग करने पर संख्या पूर्ण वर्ग बन जाएगी।

20. The average of the two numbers is 7.5 and the square root of their product is 6. Those are numbers.

दो संख्याओं का औसत 7.5 है और उनके गुणनफल का वर्गमूल 6 है। वे संख्याएँ हैं।

1. 13, 2

2. 9, 6

3. 10, 5

4. 12, 3

... Answer is 4)
Let the numbers|माना संख्याएँ = x, y
\(\therefore \frac{x+y}{2}=7.5\)
x + y = 7.5✕2
x + y = 15....(1)
xy = 6² = 36.....(2)
from eq. 1 and 2|समीकरण 1 और 2 से,
x(15 -x) = 36
15x - x² = 36
x² - 15x + 36 = 0
x² - 12x - 3x + 36 = 0
x(x - 12) -3(x - 12) = 0
(x - 12)(x - 3) =0
x = 12, 3
Shortcut- Do it through mental action.इसे मानसिक क्रिया द्वारा करें।
x + y = 15, xy = 36
x + y = 12 + 3, xy = 12 ✕ 3
x and y = 12, 3

21. The general of the army wants to make a square array of 36562 soldiers, after making the array, some soldiers were left. How many soldiers were left?

सेना का जनरल 36562 सैनिकों का वर्गाकार व्यूह बनाना चाहता है व्यूह बनाने के बाद कुछ सैनिक बच गए। कुल कितने सैनिक बचे?

1. 81

2. 36

3. 97

4. 65

... Answer is 1)

Total soldiers left|कुल सैनिक बचे = 81

22. What will be the square root of \(\frac{2+\sqrt{3}}{2}\)?

\(\frac{2+\sqrt{3}}{2}\) का वर्गमूल होगा?

1. \(\pm\frac{1}{\sqrt{2}}\left ( \sqrt{3}+1 \right )\)

2. \(\pm\frac{1}{2}\left ( \sqrt{3}- 2 \right )\)

3. \(\pm\frac{1}{2}\left ( \sqrt{3}- 1 \right )\)

4. None of the above||इनमें से कोई नहीं

... Answer is 4)
\(\frac{2+\sqrt{3}}{2}\)
= \(\frac{2\left ( 2+\sqrt{3} \right )}{4}\)
= \(\frac{\left ( 4+2\sqrt{3} \right )}{4}\)
= \(\frac{\left ( 3 + 1 +2\sqrt{3} \right )}{4}\)
= \(\frac{\left (\sqrt{3} \right )^{2}+1^{2}+2\times \sqrt{3}\times 1}{4}\)
= \(\left ( \frac{\sqrt{3}+1}{4} \right )^{2}\)
= \(\therefore \sqrt{\frac{2+\sqrt{3}}{2}}=\pm \frac{\sqrt{3}+1}{2} \)
= \(\pm\frac{1}{2}\left ( \sqrt{3}+ 1 \right )\)

23. If p = 999, then the value of \(\sqrt[3]{p(p^{2}+3p+3)+1}\)will be?

यदि p = 999 हो, तो \(\sqrt[3]{p(p^{2}+3p+3)+1}\) का मान होगा?

1. 1000

2. 999

3. 998

4. 1002

... Answer is 1)
\(\sqrt[3]{p(p^{2}+3p+3)+1}\)
= \(\sqrt[3]{p^{3}+3p^{2}+3p+1}\)
= \(\sqrt[3]{p^{3}+3p^{2}+3p+1}\)
= \(\sqrt[3]{(p+1)^{3}}\)
p + 1 = 999 + 1 = 1000

24. What will be the value of (1001)³?

(1001)³ का मान क्या होगा?

1. 1003003001

2. 100303001

3. 100300301

4. 103003001

... Answer is 1)
(1001)²
= 1002001
See the pattern|पैटर्न को देखें
(1001)³
1003003001

25. Find the least number by which the quotient obtained by dividing 625 is a perfect cube root.

वह लघुत्तम संख्या ज्ञात कीजिए जिसके द्वारा 625 में भाग दी जाने पर भागफल पूर्ण घनफल हो।

1. 25

2. 5

3. 2

4. 3

... Answer is 2)
625 = 5 ✕ 5 ✕ 5 ✕ 5
= 5³ ✕ 5
Divide by 5 to make a perfect cube|पूर्ण घन बनाने के लिए 5 से भाग देना होगा
625 ÷ 5 = 125 = 5³

26. The sum of the cubes of two numbers is 793. If the sum of the numbers is 13, then find the difference between the two numbers.

दो संख्याओं के घनों का योग 793 है। संख्याओं का योग 13 है, तो दोनों संख्याओं का अंतर बताइए।

1. 7

2. 6

3. 5

4. 8

... Answer is 3)
Let the numbers|माना संख्याएँ = x, y
where x > y
x³ + y³ = 793
and x + y = 13
∴(a + b)³ = a³ + b³ + 3ab(a + b)
(13)³ = 793 + 3xy✕13
2197 = 793 + 39xy
\(xy = \frac{1404}{39}=36\)
∴(a - b)² = (a + b)² - 4ab
= (13)² - 4 ✕ 36
= 169 - 144 = 25
\((a - b) = \sqrt{25}=5\)

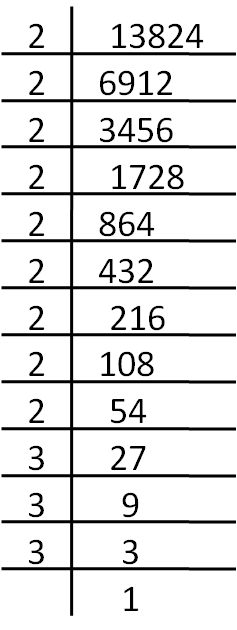
27. Find the cube root of (-13824).

(-13824) का घनमूल ज्ञात कीजिए।

1. 38

2. -38

3. 24

4. -24

... Answer is 4)

∴13824 = 2³ ✕ 2³ ✕ 2³ ✕ 3³
∴\(\sqrt[3]{-13824}=\sqrt[3]{(-1)^{3}(2)^{3}\times2^{3}\times2^{3}\times3^{3} }\)
= -1 ✕ 2 ✕ 2 ✕ 2 ✕ 3 = -24

28. If the square root of x is the cube root of y, then the relation between x and y is.

यदि x का वर्गमूल y का घनमूल है तो x और y के बीच सम्बन्ध है।

1. x³ = y²

2. x² = y³

3. x = y

4. x⁶ = y⁵

... Answer is 1)
\(\sqrt{x}=\sqrt[3]{y}\)
\(x^{\frac{1}{2}}=y^{\frac{1}{3}}\)
\(\left ( x^{\frac{1}{2}} \right )^{6}=\left ( y^{\frac{1}{3}} \right )^{6}\)
\(x^{3}=y^{2}\)

29. The difference between \(\frac{3}{4}\) and \(\frac{4}{7}\) of a number is 100, what will that number be?

किसी संख्या के \(\frac{3}{4}\) तथा \(\frac{4}{7}\) का अंतर 100 है वह संख्या क्या होगी?

1. 520

2. 540

3. 500

4. 560

... Answer is 4)
Let the number|माना संख्या = x
\(\frac{3}{4}x -\frac{4}{7}x\) = 100
21x - 16x = 2800
5x = 2800
x = 560

30. 10^3x = 125, then what will be the value of 10^-2x?

यदि 10^3x = 125 हो, तो 10^-2x का मान क्या होगा?

1. \(\frac{1}{5}\)

2. \(\frac{1}{25}\)

3. 25