Geometry, properties, mensuration formula 2D

Geometry 2D(Two Dimension)

The geometry comes from ancient Greek Geōmetría. It is made from two words Geō means 'earth or land' and metría means 'measurement' combined word meaning is 'land measurement'. Geometry deals with size, length, height and parameters e.t.c in different types of shapes. This article discusses 2D shapes like circles, triangles, squares and quadrilaterals e.t.c. 

Triangle

A triangle is a type of polygon with three sides, three angles and three vertices. There are many types of triangles.

Area of triangle = \( \frac {1}{2}✕base✕height \)

Area of the triangle when two sides and corresponding angle are given,

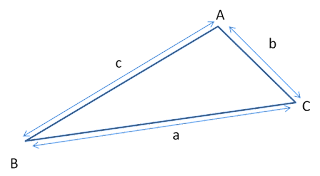
Area of △ABC = ½ ab sin C 

Area of △ABC = ½ bc sin A

Area of △ABC = ½ ac sin B

General Properties of the triangle

• In any triangle, the sum of the two smaller sides is greater than the third side.
• In any triangle, the difference between the two smaller sides is greater than the third side.
• In a triangle, the side opposite the largest angle is the longest and the side opposite the smallest angle is the shortest.
• The exterior angle of any triangle is equal to the sum of the interior opposite angles.

∠CAB + ∠ABC = ∠ACD

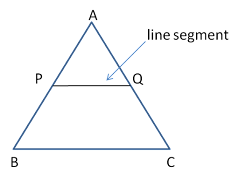
• The line segment obtained by joining the mid-point of any two sides in a triangle is parallel to the third side and is half of it.

PQ = ½ (BC)

PQ ∥ BC

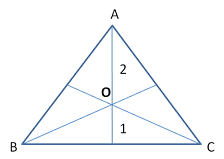
• The centroid divides the triangle into three equal parts.

Area of △ABC: Area of △AGB

3: 1

• The area of the triangle formed by joining the midpoints of the sides of the triangle is one-fourth of the area of the main triangle and the perimeter is half of the main triangle.

Area of △PQR = ¼ (Area of △ABC)

The perimeter of △PQR = ½ (Perimeter of △ABC)

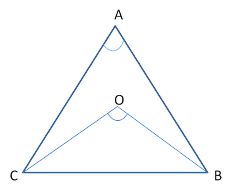
• The angle at the centre of the circle is twice the angle at the circumference.

If point O is the circumcentre of △ABC then,

∠BOC = 2∠A

• If O is the Ortho centre of △ABC then,

∠BOC + ∠A = 180°

∠BOC = 180° - ∠A

Conditions for the construction of a triangle-

• If the lengths of the three sides of the triangle are given.
• If two sides of a triangle and the angle between them are given.
• If the length of any two angles and one side of the triangle are given.

It is possible to draw a triangle if any of the three conditions are met.

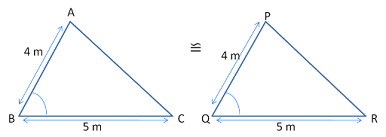
Congruence of triangles

when two triangles cover each other completely, then it can be said that both triangles are congruent with each other.

Congruence rules in the triangle

1. Side-Side-Side rule (S-S-S)-

If the corresponding sides of the two triangles are equal then the triangles are congruent.

AB = PQ

AC = PR

BC = RQ

△ABC ≅ △PQR

2. Side-angle-side rule (S-A-S)-

When two corresponding sides and the angle between them are equal then the triangles are congruent.

AB = PQ

∠B = ∠Q

BC = QR

△BAC ≅ △QPR

3. Angle-side-Angle rule (A-S-A/S-A-A/A-A-S)-

When any two angles and one side are equal then the triangles are congruent.

∠B = ∠Q

BC = QR

∠C = ∠R

△BAC ≅ △QPR

4. Right-angle - Hypotenuse - Side rule (R-H-S)-

In this rule, If in two triangles have one angle right angle, one side is equal and the hypotenuse is also equal then triangles are called congruent.

∠B = ∠Q = 90°

AC = PR

AB = PQ

△BAC ≅ △QPR

Similarity of triangles

Two triangles will be similar. If their corresponding sides are proportional and the corresponding angles are equal.

Rule of similarity of triangles

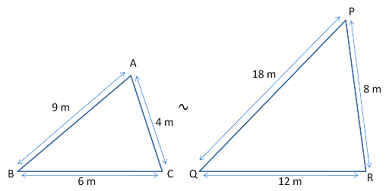
1. Side-Side-Side rule (S-S-S)-

 If the ratios of the corresponding sides of the triangle are equal then triangles are similar triangles.

\( \frac {AB}{PQ} = \frac {BC}{QR} = \frac {AC}{PR} \)

\( \frac {9}{18} = \frac {6}{12} = \frac {4}{8} \)

\( \frac {9}{18} = \frac {6}{12} = \frac {4}{8} = \frac {1}{2} \)

\( \frac {AB}{PQ} = \frac {BC}{QR} = \frac {AC}{PR} = \frac {1}{2} \)

△ABC ∼ △PQR

2. Side-angle-side rule (S-A-S)-

when the ratios of the two corresponding sides are equal and the angle between them is also equal then triangles similar.

∠B = ∠Q = 50°
\( \frac {AB}{PQ} = \frac {BC}{QR} \)

\( \frac {9}{18} = \frac {6}{12} \)

\( \frac {9}{18} = \frac {6}{12} = \frac {1}{2} \)

\( \frac {AB}{PQ} = \frac {BC}{QR} = \frac {1}{2} \)

△BAC ∼ △QPR

3. Angle-Angle-Angle rule (A-A-A) or Angle-Angle rule(A-A)-

If any two angles of triangles are equal then triangles are similar.

∠B = ∠Q = 50°
∠A = ∠P = 40°

△BAC ∼ △QPR

👉 All congruent triangles are similar but not all similar triangles are congruent.

Type of triangle on the basis of the angle

1. Acute-angle triangle

A triangle whose all three angles are less than  90°. 

a² + b² > c²

2. Right-angle triangle

A triangle whose one angle is 90° is called a right-angled triangle.

a² + b² = c²

3. Obtuse-angle triangle

A triangle in which one of the angles is greater than 90° is called an obtuse triangle.

a² + b² < c²

Type of triangle basis on sides length

1. Equilateral triangle

A triangle in which all the sides are equal is called an equilateral triangle.

Properties-

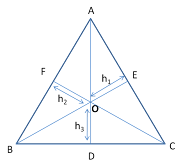
• In an equilateral triangle, the median/altitude/height is the same. 
• In an equilateral triangle, the mid-point of the median divides the median/height into 2:1.
• All angles in an equilateral triangle are 60°.

If OD = h₁ , OE = h₂ and OF = h₃ and all sides AB = AC = BC = a and height of equilateral triangle AD = h then,

Area of △ABC = Area of △BPC + Area of △CPA + Area of △APB

½ ha = ½ h₁a + ½ h₂a + ½ h₃a

½ h a = ½ a (h₁+ h₂ + h₃)

h = h₁+ h₂ + h₃

Formulas-

The perimeter of an Equilateral triangle = 3 ✕ side

Median/altitude/height of Equilateral triangle = \( \frac {\sqrt 3}{2} \times side \)

Area of Equilateral triangle =  \( \frac {\sqrt 3}{4} \times {(side)}^2 \)

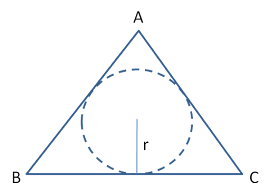
Incircle in Equilateral triangle-

Incircle radius (r) = \( \frac {side}{2 \sqrt 3} \)

Area of Incircle = πr²

= π\( (\frac {side}{2 \sqrt 3})^2 \)

= π\( \frac {{(side)}^2}{12} \)

Circumcircle in Equilateral triangle-

Circumcircle radius (R) = \( \frac {side}{ \sqrt 3} \)

Area of Incircle = πR²

= π\( (\frac {side}{ \sqrt 3})^2 \)

= π\( \frac {{(side)}^2}{3} \)

👉 Ratio of the Radius of Incircle and Circumcircle in Equilateral triangle = 1:2

👉 Ratio of the Area of Incircle and Circumcircle in Equilateral triangle = 1:4

2. Isosceles triangle

In an isosceles triangle, two sides are equal and the corresponding angles are also equal.

Formula-

The perimeter of the isosceles triangle = 2b + a

The altitude of the isosceles triangle = \( \frac {1}{2} \sqrt {4b^2 - a^2} \)

Area of Isosceles triangle = \( \frac {a}{4} \sqrt {4b^2 - a^2} \)

3. Scalene triangle

A scalene triangle has no equal sides and no angles equal.

Formula-

The perimeter of the Scalene triangle = a + b + c

(Heron's formula) Area of Scalene triangle = \( \sqrt {S(S - a)(S - b)(S - c)} \)

       Where S(Half Perimeter) = \( \frac {a+b+c}{2} \)

Area of Scalene triangle = \( \frac {4}{3} \sqrt {S_m(S_m - M_1)(S_m - M_2)(S_m - M_3)} \)

           Where S_m = \( \frac {M_1+M_2+M_3}{2} \), M₁,M₂,M₃ are medians of triangle

Circle

The locus of a point whose distance from a fixed point is always the same is called a circle.

Properties-

• An infinite number of circles can be drawn passing through one or two non-collinear points. 
• Only one circle can be drawn passing through three non-collinear points.

• Three cases when a circle can be real, point or imaginary-

case(I) - If r > 0 then, circle is Real.

case(II) - If r = 0 then, circle is a Point.

case(III) - If r < 0 then, circle is Imaginary.

Formula-

Circumference of the circle = 2πr

Area of the circle = πr²

Semicircle

Circumference of the Semicircle = πr + 2r

Area of the Semicircle = \( \frac {πr^2}{2} \)

Sector of circle

The area enclosed by two radii of a circle and the arc between them is called a sector.

Formula-

The arc length of the minor sector (l) = rθ = \( \frac {2πrθ}{360^o} \)

Circumference of minor sector = \( \frac {2πrθ}{360^o} +2r \)

Area of minor sector = \( \frac {πr^2θ}{360^o} \) = \( \frac {1}{2} ✕ arc ✕ radius \)

The arc length of the major sector (l) = rθ = \( 2πr - \frac {2πrθ}{360^o} \)

Circumference of major sector = \( 2πr - \frac {2πrθ}{360^o} +2r \)

Area of major sector = \( πr^2 - \frac {πr^2θ}{360^o} \) = \( \frac {1}{2} ✕ arc ✕ radius \)

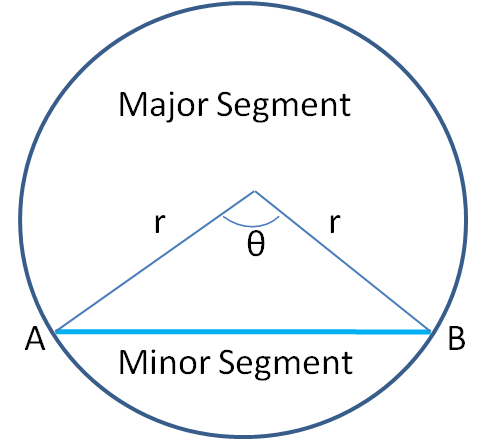
Segment of circle

A region in a circle bounded by a chord and arc (part of the circle) is called a segment.

Formula-

Circumference of minor segment = \( \frac {2πrθ}{360^o} + chord(AB) \)

Area of minor segment = \( \frac {πr^2θ}{360^o} - \frac {1}{2} r^2 sin θ \)

Circumference of major segment = \( 2πr - \frac {2πrθ}{360^o} + chord(AB) \)

Area of major segment = \( πr^2 - \left ( \frac {πr^2θ}{360^o} - \frac {1}{2} r^2 sin θ \right ) \)

Quadrilateral

The quadrilateral is a polygon that has four sides and four corners.

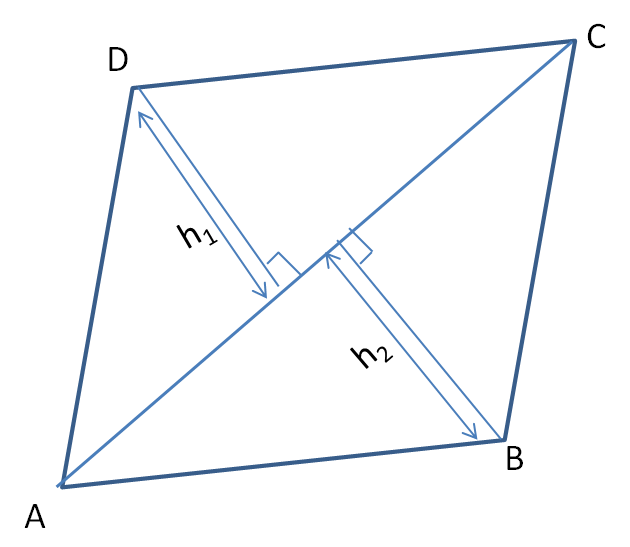
The general formula of area = ½ ✕ Diagonal ✕ the sum of the perpendiculars on the diagonal 

 = \( \frac {1}{2} ✕ AC ✕ (h_1+h_2) \)

Type of quadrilateral on the basis of angle-

Convex quadrilateral

Each interior angle is smaller than 180°.

Both of the diagonals lie inside the quadrilateral.

Concave quadrilateral

At least one interior angle is greater than 180°.

One diagonal is inside the quadrilateral and the other is outside the quadrilateral.

Type of quadrilateral-

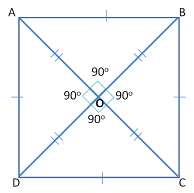
Square

All four sides of the square are equal and each angle is 90°.

Properties-

AB ∥ CD,  AD ∥ BC

AB = BC = CD = DA

∠A = ∠B = ∠C = ∠D = 90°

Diagonal AC = Diagonal BD

AO = OB = OC = OD

∠AOB = ∠BOC = ∠COD = ∠DOA = 90° (diagonal perpendicularly bisect to each other )

∠DAB + ∠ABC = ∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = 180° (The sum of the two interior angles on the same side is 180°)

Formulas- 
Perimeter = 4 ✕ side

Area = (side)² = ½ ✕ (diagonal)²

Diagonal = \( side \sqrt {2} \)

Rhombus

Its four sides are also equal and the diagonals perpendicularly bisect each other.

Let,  AC = d₁ , BD = d₂ and AB = BC = CD = DA = a

Properties-

AB ∥ CD,  AD ∥ BC

AB = BC = CD = DA

AO = OC, OB = OD

∠AOB = ∠BOC = ∠COD = ∠DOA = 90° (diagonal perpendicularly bisect to each other )

(d₁)² + (d₂)² = 4(a)²

∠DAB + ∠ABC = ∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = 180° (The sum of the two interior angles on the same side is 180°)

Formulas- 
Perimeter = 4 ✕ side = \( 2 \sqrt {{d_1}^2 + {d_2}^2 } \)

Area =  ½ ✕ Product of diagonals =  ½ ✕ AC ✕ BD 

or, Area = ½ ✕ base ✕ height

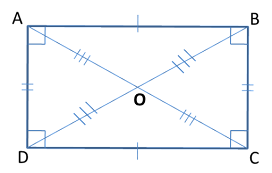
Rectangle

In this, opposite sides are equal and all angles are 90°.

Properties-

AB ∥ CD,  AD ∥ BC

AB = CD,  AD = BC

∠A = ∠B = ∠C = ∠D = 90°

Diagonal AC = Diagonal BD

AO = OB = OC = OD

∠DAB + ∠ABC = ∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = 180° (The sum of the two interior angles on the same side is 180°)

Formulas- 
Perimeter = 2 ✕ (length + breadth)  = 2 ✕ (AB + BC)

Area =  length + breadth 

Diagonal = \( \sqrt {(length)^2 + (breadth)^2} \)

Parallelogram

In this, the opposite sides are parallel and equal.

Let,  AC = d₁ , BD = d₂ and AB = DC = a, BC = AD = b

Properties-

AB ∥ CD,  AD ∥ BC

AB = CD,  AD = BC

AO = OC, OB = OD

(d₁)² + (d₂)² = 2(a² + b² )

∠DAB + ∠ABC = ∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = 180° (The sum of the two interior angles on the same side is 180°)

Formulas- 
Perimeter = 2 ✕ (a + b)  

Area = base ✕ height

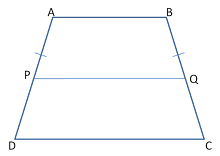
Trapezoid 

In this, two sides are parallel and the other two sides are equal.

Properties-

AB ∥ CD

AD = BC

∠A + ∠C = ∠B + ∠D = 180°

∠DAB + ∠ABC = ∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = 180° (The sum of the two interior angles on the same side is 180°)

Formulas- 
Perimeter = Sum of all four sides = AB + BC + CD + DA

Area = ½ ✕ sum of parallel sides ✕ distance between parallel sides 

👉 If P and Q are mid-point of side AD and BC respectively and AB ∥ PQ ∥ CD then,

PQ = \( \frac {CD+AB}{2} \)

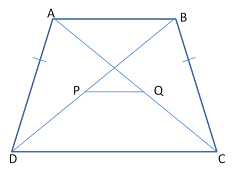
👉 If P and Q are mid-point of the diagonals BD and AC respectively and AB ∥ PQ ∥ CD then,

PQ = \( \frac {CD-AB}{2} \)

Cyclic quadrilateral

If all the vertices of a quadrilateral touch the circumference of a circle. So that quadrilateral is called a cyclic quadrilateral.

Properties-

• Any exterior angle of a cyclic quadrilateral is equal to the interior angle opposite its vertex.

∠BCO = ∠DAB

• ∠A + ∠C = 180°,  ∠B + ∠D = 180° 

Formula-

Area of cyclic quadrilateral = \( \sqrt {(S-a)(S-b)(S-c)(S-d)} \)

Where S = \( \frac {a+b+c+d}{2} \)

Kite

In Kite symmetry with respect to vertical diagonal.

Properties-

AB = AD,  BC = CD

90°  angle between diagonals. (AC ⊥ BD)

OB = OD