Coordinate Geometry
Coordinate Geometry functions and formulas or Identity list
This is for all competitive exams like SSC, Railway, Bank, TGT, PGT and other competitive exams and academic exams like intermediate or High school exam CBSE, ICSE (class 10, 11, 12) or State board.
UPI ID:- achalup41-1@oksbi
Contact Email ID:- achalup41@gmail.com
Coordinate Plane or Cartesian plane
It helps to locate any point in 2-D space. Some essential terms are given below.
Origin- It is the centre point of the cartesian plane and it is generally denoted by 'O' and coordinate (0, 0).
Abscissa- It is the value of distance on the X-axis. It denotes value from the origin negative and positive sides on the X-axis.
Ordinate- It is the value of distance on the Y-axis. It denotes value from the origin negative and positive sides on the Y-axis.
Cartesian Coordinate
It is in the form (x, y).
e.g.- (2, 3), (3, 4), (5, 8) e.t.c
Polar Coordinate
It is in the form (r, θ).
Where,
cos θ = \(\frac {x}{r}\) ⇒ x = r cos θ
sin θ = \(\frac {y}{r}\) ⇒ y = r sin θ
tan θ = \(\left|\frac{y}{x}\right|\) ⇒ θ = \(tan^{-1}\left|\frac{y}{x}\right|\)
r = \( \sqrt {x^2 + y^2}\)
e.g.- \((2, \frac {π}{2})\), \((5, \frac {π}{6})\)), (8, 60°), (3, 45°) e.t.c
Distance formula
Cartesian form
Let the two-point P(x, y) and Q(x, y) then the distance between PQ.
PQ = \(\sqrt {(x_2 - x_1)^2 + (y_2 - y_1)^2}\)
Polar form
PQ = \(\sqrt {(r_1)^2 + (r_2)^2 - 2r_1r_2cos (θ_1 - θ_2)}\)
Straight Line Equations
i. General form
ax + by + c = 0👉 Slope of the equation = \(-\frac {coefficient \space of \space 'a'}{coefficient \space of \space 'b'}\) = \(-\frac {a}{b}\)
ii. Slope form
y = mx + CWhere,
m(slope) = tan θ
C = Intersection cut on Y-axis
iii. Intercept form
\(\frac {x}{a} + \frac {y}{b} = 1\)
where,
a = Intersection cut on X-axis
b = Intersection cut on Y-axis
iv. Normal Form
x cos α + y sin α = pwhere,
p = The length of the perpendicular 'OM' from the origin to the line.
α = Angle between normal (OM) and X-axis.
Slope of a line
The formula of the slope if a line passes through two points (x1, y1) and (x2, y2)m = \(\frac {y_2 - y_1}{x_2 - x_1}\)
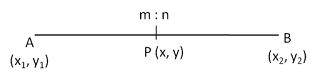
Section Formula or Division formula
A point (x, y) divides the line segment by joining the points (x1, y1) and (x2, y2) in the ratio m : n then,
i. Internal Division-
p (x, y) = \((\frac {mx_2 + nx_1}{m+n}, \frac {my_2 + ny_1}{m+n})\)
ii. External Division-
p (x, y) = \((\frac {mx_2 - nx_1}{m-n}, \frac {my_2 - ny_1}{m-n})\)Mid-Point Formula
p (x, y) = \((\frac {x_2 + x_1}{2}, \frac {y_2 + y_1}{2})\)
Equation of line passing through a point
Equation of line passing through the point (x1, y1) is,
y - y1 = m (x - x1)
where, m = slope
Equation of line passing through two points
Equation of line passing through two points (x1, y1) and (x2, y2) is,
y - y1 = \(\frac {y_2 - y_1}{x_2 - x_1}\) (x - x1)
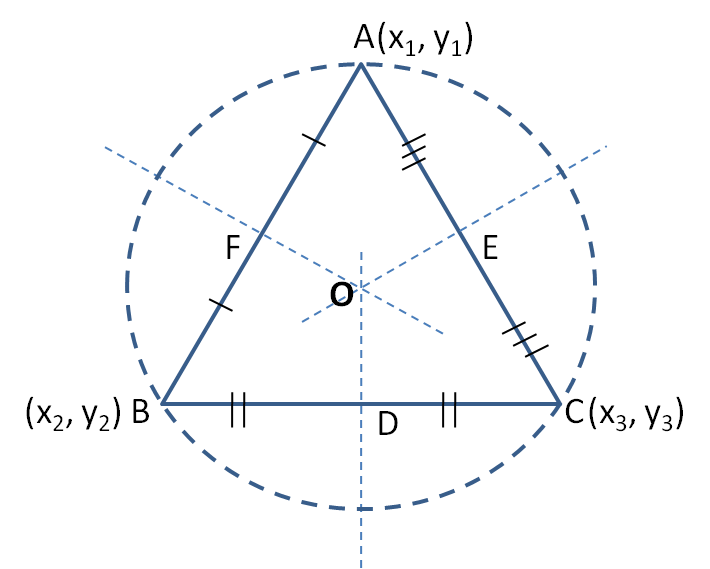
Centroid of Triangle
The point of intersection of the medians of a triangle is called the centroid. The centroid divides the median in the ratio 2 : 1 internally.
G \((\frac {x_1+x_2+x_3}{3}, \frac {y_1+y_2+y_3}{3})\)
In-centre of triangle
The point of intersection of the interior angle bisectors of a triangle is called the In-centre and it is located at an equal distance from the sides of the triangle.
I \((\frac {ax_1+bx_2+cx_3}{a+b+c}, \frac {ay_1+by_2+cy_3}{a+b+c})\)Circum-centre of triangle
The point of intersection of the perpendicular bisectors of the sides is called the circum-centre of the triangle.
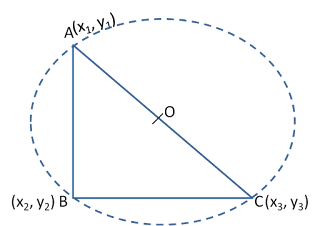
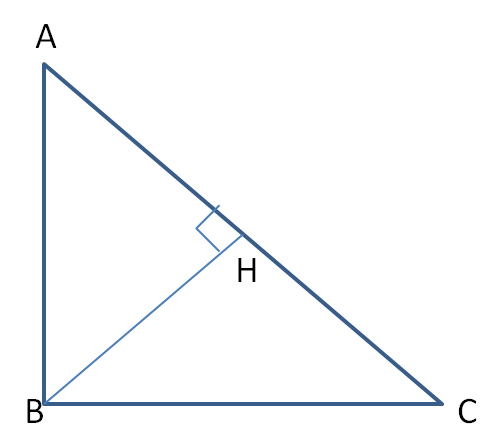
Ortho centre in triangle
The point of intersection of the altitudes is called the Ortho centre of the triangle.
Note-
Ortho centre in Right angle triangle-
Ex-centre in Triangle
The circle which touches the triangle from the outside with all three sides, its centre is called the ex-centre.
I1 \((\frac {-ax_1+bx_2+cx_3}{-a+b+c}, \frac {-ay_1+by_2+cy_3}{-a+b+c})\)
I2 \((\frac {ax_1-bx_2+cx_3}{a-b+c}, \frac {ay_1-by_2+cy_3}{a-b+c})\)
I3 \((\frac {ax_1+bx_2-cx_3}{a+b-c}, \frac {ay_1+by_2-cy_3}{a+b-c})\)
Perpendicular distance between two parallel lines
If two parallel lines are ax + by + c1 = 0 and ax + by + c2 = 0 then perpendicular distance between these two lines,
d = \(\left | \frac {c_1 - c_2}{\sqrt {a^2+b^2}} \right | \)
Perpendicular distance of a line from a point
If point is (x1, y1) and line is ax + by + c = 0 then perpendicular distance from the point,
d = \(\left | \frac {ax_1 + by_1 + c}{\sqrt {a^2+b^2}} \right | \)
Angle between two lines
If slope of two lines m1 and m2 respectively then the angle,
tan θ = \(\left | \frac {m_1 - m_1}{\sqrt {1+m_1m_2}} \right | \)
Concurrent lines
If three equations a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 and a3x + b3y + c3 = 0 are concurrent then
\[ \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix} =0 \]
General quadratic equation
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
General equation For circle
If h = 0 and a = b
x2 + y2 + 2gx + 2fy + c = 0
Centre (-g, -f)
Radius r = \(\sqrt {g^2 + f^2 - c}\)
Equation of circle central form
OP = r
\(\sqrt {(x-α)^2+(y-β)^2} = r\)
(x-α)2+(y-β)2 = r2
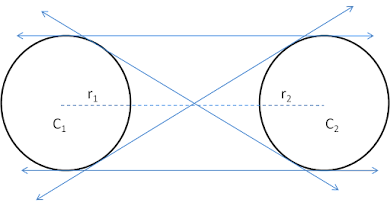
Position of two circles and tangent
case I-
If c1c2 > r1 + r2
Number of common tangents = 4
Case II-
If c1c2 = r1 + r2
Number of common tangents = 3
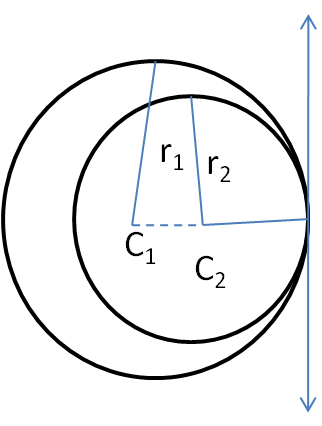
case III-
If r1 - r2 < c1c2 < r1 + r2
Number of common tangents = 2
case IV-
If r1 - r2 = c1c2
Number of common tangents = 1
case V-
If c1c2 < r1 - r2
Number of common tangents = 0
Don't forget to share with friends and support🙏
Logarithms (exponential and logarithmic series)
Average Definition and formulas
Average Questions with solution
Inverse Trigonometric function formulas pdf







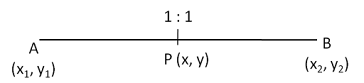









Post a Comment
Please do not enter any site link in the comment box 🚫.