Number System | Free pdf

Donate me through 👇

UPI ID:- achalup41-1@oksbi

Number system

With the development of mathematics, many number systems were developed. The numbers used in each number system are different and their bases are also different. Generally, a number system is named on the basis of the total number of digits contained in it. Some of the popular number systems are as follows-

1. Binary Number System
2. Decimal Number System
3. Octal Number System
4. Hexadecimal Number System

Binary Number System

In the binary numeral system, only two digits 0 and 1 are used, so 2 is used in its base, 0 or 1 is called a bit. 

1 Byte = 8 Bits

The binary numeral system is also called the 'Place-Value system' because in this each binary digit has its own value which we represent as a power of 2 The value of the power of 2 increases from right to left goes.

Those which are on the left in the binary numeral system, represent Integer. The first bit on the left is of the largest value. That's why it is called the Most Significant Bit (MSB). The last bit on the right has the smallest value, so it is called the Least Significant Bit (LSB). 

Example 1- Convert (63)₁₀ to a binary number.

Solution- 

Hence, (63)₁₀ = (111111)₂

Example 2- Convert (63.125)₁₀ to a binary number.

Solution- 

First step- Converting integer part to binary number by simple method-

(63)₁₀ ⟶ (111111)₂

Second step- The binary conversion of the fractional part is as follows.

(.125)₁₀ ⟶ (.001)₂

Hence, (63.125)₁₀ = (111111.001)₂

Decimal Number System

Generally, the method of calculation we use to calculate is called the decimal number system. In this system ten digits- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 are used. It is read from left to right. The value of the digits depends on their place in the decimal numeral system. The value of the numbers increases to the left because in this system its value is fixed by the place of the number, hence it is also called the 'place value system'. For example, in the number 819, 8 represents the hundred, 1 represents the tens and 9 represents ones, so here 8 is the most significant digit (MSD) and 9 is the least significant digit (LSD). 

Left ⟶ 819 ← Right 

Example 1- Convert (111111)₂ to a decimal number.

Solution- 

= 1 ✕ 2⁵ + 1 ✕ 2⁴ + 1 ✕ 2³ + 1 ✕ 2² + 1 ✕ 2¹ + 1 ✕ 2⁰

= 32 + 16 + 8 + 4 + 2 + 1

= 63

Hence, (111111)₂ = (63)₁₀

Example 2- (111111.101)₂ को दशमलव संख्या में बदलें। 

Solution- 

First step- Converting the integer part to a decimal number by the usual method-

= 1 ✕ 2⁵ + 1 ✕ 2⁴ + 1 ✕ 2³ + 1 ✕ 2² + 1 ✕ 2¹ + 1 ✕ 2⁰

= 32 + 16 + 8 + 4 + 2 + 1

= 63

(111111)₂ ⟶ (63)₁₀

Second step- The decimal conversion of the fractional part is as follows, in which the negative power of 2 is multiplied by adding them. On moving from left to right, the negative power of 2 increases gradually.

= 1 ✕ 2^-1 + 0 ✕ 2^-2 + 1 ✕ 2^-3 

= 1 ✕ ¹⁄₂ + 0 ✕ ¹⁄₄ + 1 ✕ ¹⁄₈ 

= 0.5 + 0 + 0.125

= 0.625

(.101)₂ ⟶ (.625)₁₀

Hence, (111111.101)₂ = (63.625)₁₀

Octal Number System

The octal numeral system uses the eight digits 0, 1, 2, 3, 4, 5, 6, 7 The base of this numeral system is 8. A digit in the octal numeral system represents a group of three binary digits. Following is the table of octal numeral system-

Octal Number	Binary Number
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Example 1- Convert (98)₁₀ to octal number.

Solution- 

Hence, (98)₁₀ = (142)₈

Example 2- Convert (1101)₂ to octal number.

Solution- 

(1101)₂ = 1 ✕ 2³ + 1 ✕ 2² + 0 ✕ 2¹ + 1 ✕ 2⁰ 

= 8 + 4 + 0 + 1 = 13

(1101)₂ ⟶ (13)₁₀

Now, (13)₁₀

(13)₁₀ ⟶ (15)₈

Hence, (1101)₂ = (15)₈

Second method- In this, 1101 will be combined into pairs of three bits. 

001 101 (The number 0 on the left is used to complete a three bits pair.)

(1 5)₈   (On keeping the equivalent value from the table)

Hence, (1101)₂ = (15)₈

Example 3- Convert (98.95)₁₀ to an octal number.

Solution- 

First step- Converting integer part to octal number by simple method-

Look at Example 1 of Octal Number.

(98)₁₀ ⟶ (142)₈

Second step- The conversion of fractional part into octal number is as follows-

Mainly this process is repeated for up to three digits only. 

(.95)₁₀ ⟶ (.746)₈

Hence, (98.95)₁₀ = (142.746)₈

Example 4- Convert (142.746)₈ to a decimal number.

Solution- 

First step- Converting the integer part from octal number to decimal number is done in the following way-

= 1 ✕ 8² + 4 ✕ 8¹ + 2 ✕ 8⁰ 

= 64 + 32 + 2 = 98

(142)₈ ⟶ (98)₁₀

Second step- The conversion of fractional part from octal number to decimal number is as follows-

= 7 ✕ 8^-1 + 4 ✕ 8^-2 + 6 ✕ 8^-3 

= 7 ✕ ¹⁄₈ + 4 ✕ ¹⁄₆₄ + 6 ✕ ¹⁄₅₁₂ 

= 0.875 + 0.0625 + 0.0117

= 0.9492 ≈ 0.95

(.746)₈ ⟶ (.95)₁₀

Hence, (142.746)₈  = (98.95)₁₀ 

Hexadecimal Number System

The base of numbers in the hexadecimal numeral system is 16. With the help of this system, information is shown in a short form, nowadays this system is being used in big computers, in this system 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F up to 16 letters are used. A, B, C, D, E, and F are used in place of 10, 11, 12, 13, 14, and 15 respectively. This is done because all the digits after 9 come under the decimal system. 

Relation table among Binary, Octal, Decimal and Hexadecimal Number System

The relationship table is as follows-

Binary	Octal	Decimal	Hexadecimal
0000	0	0	0
0001	1	1	1
0010	2	2	2
0011	3	3	3
0100	4	4	4
0101	5	5	5
0110	6	6	6
0111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

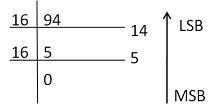
Example 1- Convert (94.95)₁₀ to a hexadecimal number.

Solution- 

First Step- Converting the integer part to hexadecimal is done as follows-

(94)₁₀ ⟶ (5E)₁₆     (14 is represented by E. See above table)

Second Step- The conversion of the fractional part to hexadecimal is as follows-

(.95)₁₀ ⟶ (.F33)₁₆  

Hence, (94.95)₁₀  = (5E.F33)₁₆ 

Example 2- Convert (5E.F33)₁₆ to a decimal number.

Solution- 

First Step- Converting the integer part to a decimal number by the usual method-

= 5 ✕ 16¹ + E ✕ 16⁰

= 5 ✕ 16¹ + 14 ✕ 16⁰

= 80 + 14 ✕ 1

= 94

(5E)₁₆ ⟶ (94)₁₀

Second Step- The decimal conversion of the fractional part is as follows-

= F ✕ 16^-1 + 3 ✕ 16^-2 + 3 ✕ 16^-3 

= 15 ✕ ¹⁄₁₆ + 3 ✕ ¹⁄₂₅₆ + 3 ✕ ¹⁄₄₀₉₆ 

= 0.9375 + 0.01171 + 0.0007324

= 0.9499  ≈ 0.95

(.F33)₁₆ ⟶ (.95)₁₀

Hence (5E.F33)₁₆ = (94.95)₁₀

Types of Numbers

Numbers are divided into several parts on the basis of their nature and structure which are as follows.

Natural numbers

The numbers used to count anything are called natural numbers.

Peano's postulates- "Numbers used to count things."

It is denoted by 'N'.

N = {1, 2, 3, 4, 5, ............∞}

Integers

The set from -∞ to ∞ is called an integer, it is represented by 'Z'. Z is used for the German word 'Zahlen' which means 'numbers' or 'to count'.

Z = {-∞, ...........-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 .........., ∞}

Integer numbers can be classified into positive and negative integers. Positive integers are denoted by Z⁺ and negative integers are denoted by Z^-.

Z^- = {-∞, ...........-5, -4, -3, -2, -1}

Z⁺ = {1, 2, 3, 4, 5 .........., ∞}

Qus- If a and b are any two integers, will a^b be integers?

a^b = 0⁰ (undefined)

5^-2 = ¹⁄₂₅ = 0.04

This is not true because it becomes undefined if the value is 0.

Whole Numbers

When 0 is also included in the natural numbers, the set becomes the set of whole numbers, it is denoted by 'W'. 

W = {0, 1, 2, 3, 4, 5 .........., ∞}

Even Numbers

The natural numbers which are divisible by 2 are called even numbers, it is mostly represented by 'E'.

E = {2, 4, 6, 8, ............, ∞}

Odd Numbers

Those numbers which are not exactly divisible by 2 are called odd numbers and are denoted by 'O'. 

O = { 3, 5, 7, 9 ............, ∞}

Divisible Number/Composite Number

Those whole numbers which have other factors other than itself and 1 or are divisible by any number other than itself and 1 are called composite numbers.

e.g. - 4, 6, 8, 9, 10 ............, ∞

The factor of 4 = 1, 2, 4

The factor of 9 = 1, 3, 9

➡ The smallest composite number is '4'.

➡ The smallest odd composite number is '9'.

Prime Number

Those whole numbers which do not have any other factor other than itself and 1 or are not divisible by any number other than itself and 1 are called prime numbers.

e.g. - 2, 3, 5, 7, 11 ............, ∞

The factor of 2 = 1, 2

The factor of 3 = 1, 3

 ➡ '2' is the smallest prime number and '1' is neither a composite number nor a prime number

 ➡ '3' is the smallest odd prime number.

Co-Prime Numbers

Two prime numbers which do not have any common factor other than 1.

e.g. - (2, 5), (7, 11), (19, 13), (23, 29)

(7, 11)

7 = 1✕7

11 = 1✕11

There is no other common factor other than 1.

Relatively prime numbers

Two numbers which have no common factors other than 1 in other words whose HCF is 1.

e.g. - (4, 15), (13, 81), (19, 13), (23, 29)

(13, 81)

13 = 1✕13

81 = 1✕3✕3✕3✕3

There is no other common factor other than 1.

➡ Any two consecutive numbers can also be co-prime numbers.

(2, 3), (81, 82), (99, 100) 

➡ Sometimes a relative prime number is also called a co-prime number.

Twin Prime Number

Those prime numbers whose difference is '2' are called Twin Prime numbers.

e.g. - (3, 5), (7, 9), (9, 11), (11, 13)

Rational Number 

Numbers that can be expressed as ^p⁄_q are called rational numbers where p and q are integers, both have no common factors and q ≠ 0. 

e.g. - ²⁄₅, ¹¹⁄₇, ^-5⁄₁₁, ^√25⁄₁, ¹⁄_√36, ²²⁄₇

➡ Numbers whose decimal expansion is terminating (Terminating Decimals) or Repeating Decimals.

e.g. -  0.6578, 52.67, 0.3333.......= 0.3, 86.73586586586586.....= 86.73586

Terminating Decimals- Numbers that stop after a few digits of the decimal.

e.g. -  0.6578, 52.6758 

Repeating Decimals- Numbers in which a number or group of numbers is repeated repeatedly. 

e.g. -  0.33333.....= 0.3, 52.67582582582........= 52.67582

Irrational Numbers

Those numbers which cannot be written in the form ^p⁄_q are called irrational numbers.

e.g. -  √2, √3, √5, √(11), π [because the value of π = 3. 4159...... (approximate)]

➡ The numbers whose decimal expansion is of non-terminating decimals and non-repeating decimals are irrational numbers.

e.g. -  √2 = 1.41421356........

Qus. Convert 0.33333........ to a Rational number (Fraction number).

Let, x = 0.33333....... ----(i)

According to Question,

x= 0.333333.....

10x = 10✕0.33333.....

10x = 3.3333333.....

10x = 3 + 0.333333.........

10x = 3 + x        [From eq. '(i)']

10x - x = 3

9x = 3

x = ³⁄₉

x = ¹⁄₃

Qus. If a and b are any two rational numbers, then which of the following is a rational number?

(i) a+b    (is a rational number)

e.g- ¹⁄₃ + ²⁄₅ = ⁽⁵⁺⁶⁾⁄₁₅ = ¹¹⁄₁₅

(ii) a-b    (is a rational number)

e.g- ²⁄₃ - ¹⁄₃ = ¹⁄₃

(iii) a✕b    (is a rational number)

e.g- ²⁄₃ ✕ ⁴⁄₅ = ⁸⁄₁₅

(iv) ^a⁄_b    (is a rational number)

e.g- ⁽⁰⁾⁄₍₀₎  (undefined)

 ^(a)⁄₍₀₎  = ∞ (undefined)

(v) a^b    (is not a rational number)

e.g- (5)^(1/2) = √5 (irrational number)

(0)⁰ (undefined)

➡ There are infinite numbers of rational numbers between any two rational numbers.

➡ There are infinite irrational numbers between any two irrational numbers.

Real Number

Those rational or irrational numbers whose squared gives a positive number are called real numbers.

e.g.-  -5, -6/7 

(-5)² = 25

 (-6/7)²= 36/49

Imaginary Number or Non-Real Number

Those rational or irrational numbers whose squared gives a negative number are called Imaginary numbers, it is represented by 'i' which is called 'iota', its value is √-1.

e.g.-  √-5, √(-6/7)

√-5 = √(-1✕5) = i√5

√(-6/7) = √(-1✕6/7) = i√(6/7)

Complex Number

Complex numbers are made up of imaginary and real numbers and its denoted by a±ib.

Where, a = Imaginary number 

b = Real number

e.g.-  2+i3, 5-i6, -6+i√8

Qus. If a and b are any two real numbers, then which of the following is a real number?

(i) ^a⁄_b (is not a real number)

e.g.- 5/0 = ∞ 

(ii) a^b (is not a real number)

e.g.- (-5)^1/2 = √-5 = √(-1✕5) = i√5 (Imaginary number)

Cyclic Numbers

Such a number of 'n' digits which multiplied by any digit from '1' to the number of digits in that number and the product is made of the same number of 'n' digits.

e.g.-  142857

(Digits in number) n = 6   (1, 2, 3, 4, 5, 6)

1✕142857 = 142857

2✕142857 = 285714

3✕142857 = 428571

4✕142857 = 571428

5✕142857 = 714285

6✕142857 = 857142

Perfect Numbers

Those numbers whose factors add up to the same number except that number itself, that number is called a Perfect Number. 

e.g.-  6, 28, 496

Factors of 6 = 1, 2, 3, 6

Sum of all factors except 6 = 1+2+3 = 6

➡ 6 is the smallest Perfect number.

Factors of 28 = 1, 2, 4, 7, 14, 28

Sum of all factors except 28 = 1+2+4+7+14 = 28

Factors of 496 = 1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Sum of all factors except 496 = 1+2+4+8+16+31+62+124+248 = 496

➡ If a number is Perfect number then the sum of the reciprocals of all its factors including itself will always be '2'.

6 = 1, 2, 3, 6

¹⁄₁ + ¹⁄₂ + ¹⁄₃ + ¹⁄₆ = ^(6+3+2+1)⁄₆ = ¹²⁄₆ = 2

28 = 1, 2, 4, 7, 14, 28

¹⁄₁ + ¹⁄₂ + ¹⁄₄ + ¹⁄₇ + ¹⁄₁₄ + ¹⁄₂₈ = ^{(28+14+7+4+2+1)}⁄₂₈ = ⁵⁶⁄₂₈ = 2

Ramanujan's number or Ramanujan-Hardy number

A number that can be written as the sum of the cubes of two different types of numbers.

e.g.-  1729 

Happy Number

Sum the squares of all the digits of a number and continue this process until the final result is '1' but the numbers which do not have the final result '1' are not Happy Numbers.

e.g.-  49, 44, 13, 23, 28, 31, 82 

49 = 4² + 9² = 16+81 = 97

97 = 9² + 7² = 81+49 = 130

130 = 1² + 3² + 0² = 1+9+0 = 10

10 = 1² + 0² = 1+0 = 1

and 

28 = 2² + 8² = 4+64 = 68

68 = 6² + 8² = 36+64 = 100

100 = 1² + 0² + 0² = 1+0+0 = 1

Palindromic Number

A palindromic number is also called a numeric palindrome or a numerical palindrome. When a palindromic number is written in reverse, the number remains the same, in other words, reflected symmetry on the vertical axis.

e.g.-  (11)² = 121

(111)² = 12321

(1111)² = 1234321

or

75257

16561

Properties of Addition

Closure Property

The sum of two integer numbers will always be an integer number.

a+b = c

where a, b and c are integers.

e.g.-  4+5 = 9

3+(-2) = 1

(-4)+3 = -1

Commutative Property

According to this property Changing the position does not make any difference to the value of the number.

a+b = b+a

where a, b are integers.

e.g.-  4+5 = 9 or 5+4 = 9

(-8)+10 = 2 or 10+(-8) = 2

Associative Property

It provides the procedure for adding three or more numbers.

(a+b)+c = a+(b+c) = a+b+c

e.g.-  (4+3)+5 = 4+(3+5) = 12

Additive Identity

If a + 0 = a, hence zero is called an additive identity.

e.g.-  4+0 = 4

Additive Inverse

If a + (-a) = 0, hence both a and (-a) will be additive inverses of each other. 

e.g.-  4+(-4) = 0, so both 4 and (-4) are additive inverses of each other.

Properties of Multiplication

Closure Property

The multiplication of two integer numbers will always be an integer number.

a✕b = c

where a, b and c are integers.

e.g.-  4✕5 = 20 

3✕(-2) = -6

(-4)✕3 = -12

Commutative Property

Changing the position according to this property does not make any difference to the value of the number.

a✕b = b✕a

where a, b are integers. 

e.g.-  4✕5 = 20 or 5✕4 = 20

(-8)✕10 = -80 or 10✕(-8) = -80

Associative Property

It provides procedure for adding three or more numbers.

(a✕b)✕c = a✕(b✕c) 

e.g.-  (4✕3)✕5 = 4✕(3✕5) = 60

Multiplicative Identity

If a ✕ 1 = a, hence 1 is called a Multiplicative identity.

e.g.-  4✕1  = 4

Multiplicative Inverse

If a ✕ b = 1, So both a and b will be multiplicative inverses of each other.

Or, if ^x⁄_y ✕ ^y⁄_x = 1, So both ^x⁄_y and ^y⁄_x will be multiplicative inverses of each other.

e.g.-  4✕1⁄4 = 1, So both 4 and 1⁄4 are multiplicative inverses of each other.

Or, 3⁄4✕4⁄3 = 1, So both 3⁄4 and 4⁄3 are multiplicative inverses of each other.

Iterative sum of multiplication

If a number is added repeatedly, then its value is equal to the product of that number and its frequency.

a+a+a = 3✕a

e.g.-  4+4+4 = 3✕4 = 12

Divison Operation in Numbers

Let 'q' be the quotient and the remainder 'r' on dividing a number 'a' by a number 'b', then

a = bq +r,    Where 0 ≤ r < b

a = Dividend

b = Divisor

q = Quotient

r = Remainder

Dividend = (Divisor ✕ Quotient) + Remainder

➡ (xⁿ - aⁿ) will always be exactly divisible by (x - a) if n is an odd number. 

➡ (xⁿ + aⁿ) is exactly divisible by (x + a) if n is an odd number.

➡ (xⁿ - aⁿ) is exactly divisible by (x + a) & (x - a) only if n is an even number.

➡ (xⁿ + aⁿ) will never divisible by (x + a) & (x - a) if n is an even number.

Download pdf

How to find the Unit digit

Divisibility Rule for 2, 3, 4, 5, 6, 7, 8, 9, 10, 11

HCF and LCM

Simplification

Simplification Questions with solution

HCF and LCM Questions

Number System Questions

Unit digit Questions