Sets (Mathematics)
Sets
In mathematics, a set is the collection of well-defined things or objects or numbers and No repetition of elements in the set i.e. one element is only one time in set. Generally set is defined in the curly bracket {} and the whole set is represented by a capital letter.
e.g.- 'A' is the set of all natural numbers.
A = {1, 2, 3, 4, 5, ............∞}
UPI ID:- achalup41-1@oksbi
Cardinal Number of a set
It is the number of elements in the set.
e.g.- set A is the set of vowels in English.
A = {a, e, i, o, u}
Cardinal number of set 'A' is n(A) = 5
Types of set representation
Generally, three types of set representation used they are:
- Semantic form
- Roster form/tabular form
- Set builder form
Semantic form
In this form set's element is defined in the statement or element described in the statement form.
e.g.- Set 'A' is the collection of the first ten even numbers.
Roster form/tabular form
That is the most common form used in mathematics. In this form set elements are defined in curly brackets and the whole set is represented by a capital letter.
e.g.- Semantic form- 'B' is the set of the first six even numbers.
Roster form- X = {2, 4, 6, 8, 10, 12}
Set builder form
The set builder form is a type of rule or statement that describe the elements in the set. In this form, we use | or : with the text or statement to describe the elements and it is called 'such that'. Let's understand by an example-
e.g.-
Roster form- B = {1, 2, 3, 4}
Set builder form- B = {x : x < 5, x ∈ N}
Where x ∈ N- 'x' belong to the natural number.
Type of sets
There are many types of sets described below
Null set/Empty set/void set
A set that does not contain any element is called a Null set. It is denoted by {} or Φ (greek alphabet phi)
e.g.- In 'A' is null set then,
A = {} or Φ
Singleton set
A set with only one element is called a singleton set.
e.g.- A = {x : 2 < x < 4, x ∈ N}
A = {3}
Finite set
A set with a finite number of elements or in words we can count the elements of a set called a finite set.
e.g.- X = {1, 3, 5, 7}
Infinite set
A set with an infinite number of elements or we can't count the total number of elements is called an infinite set.
e.g.- B = {2, 4, 6, 8, ..........................∞}
Universal set
A universal set is a set with the collection of all elements regarding the subject. and It is denoted by 'U'.
e.g.- U = {All two-digit even number}
Equal sets
Two sets with the same element are called equal sets.
e.g.- A= {2, 4, 6}
B = {4, 2, 6}
A = B
Unequal sets
If in any two sets one or more than one element is different called an unequal set.
e.g.- A = {2, 4, 6}
B = {2, 9, 6}
A ≠ B
Overlapping sets
When at least one or more than one element is common between two sets.
e.g.- A = {1, 2, 3, 4, 5, 6, 7, 8} B = {4, 5, 6, 7, 9, 10}
Here 4, 5, 6, and 7 are common elements so A and B are overlapping sets.
Disjoint sets
If two sets with no common element then they are called disjoint sets.
e.g.- A = {1, 2, 3, 4} B = {5, 6, 7, 8}
Here no common element so A and B disjoint sets.
Subset and Superset
If all elements of B are present in set A then B is called a subset of A and It is represented as B ⊆ A and Its reciprocal A is a superset of B represented as A ⊇ B.
e.g.- A = {2, 4, 6, 8, 10}
B = {2, 4}
B Subset of A- B ⊆ A
A Superset of B- A ⊇ B
Set Operations
Many types of operations in the set some operations are given below.
Complement set
If A is a set that all elements in the universal set except set A element are called complement set and it is denoted by A' or Ac
e.g.-
U = {1, 2, 3, 4, 5, 6, 7, 8}
A = {2, 4, 6}
A' = {1, 3, 5, 7, 8}
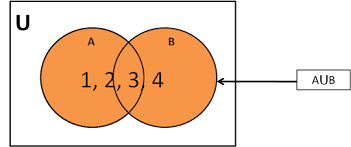
Union of sets
If A and B are two sets then the union of A and B are the set of all elements in A and B. It is represented by A⋃B.
e.g.-
A = {1, 2, 3}
B = {2, 3, 4}
A⋃B = {1, 2, 3, 4}
Intersection of sets
If A and B are two sets then the Intersection of A and B are the set of all common elements in A and B. It is represented by A⋂B.
e.g.-
A = {1, 2, 3}
B = {2, 3, 4}
A⋂B = {2, 3}
Difference in sets
If A and B are two sets then the difference (A - B) is all elements of set A except common elements in A and B.
e.g.-
A = {1, 2, 3, 5, 6}
B = {2, 3, 4}
A-B = {1, 5, 6}
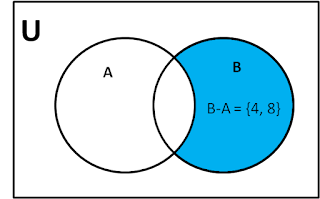
If A and B are two sets then the difference (B - A) is all elements of set B except common elements in A and B.
e.g.-
A = {1, 2, 3, 5, 6}
B = {2, 3, 4, 8}
B-A = {4, 8}
Union between three sets
You can find it by formula or Venn Diagrams
n(A⋃B⋃C) = n(A) + n(B) + n(C) - n(A⋂B) - n(B⋂C) - n(A⋂C) + n(A⋂B⋂C)
Cartesian Product
Cartesian product is the product of two sets and Its denoted by A × B.
e.g.-
A = {a, b, c}
B = {m, n}
A × B = {(a, m), (a, n), (b, m), (b, n), (c, m), (c, n)}
Note-
1. If n(A) = p and n(B) = q then,
n(A × B) = pq
2. If n(A) = p, n(B) = q, n(C) = r then,
n(A × B × C) = pqr
3. If A = Φ and B = Φ then,
A × B = Φ
4. A × (B ⋃ C) = (A × B) ⋃ (A × C)
5. A × (B ⋂ C) = (A × B) ⋂ (A × C)
Properties and Identities in sets
Identities
- n(A⋃B) = n(A) + n(B) - n(A⋂B)
- n(A⋂B) = n(A) + n(B) - n(A⋃B)
- n(A⋃B⋃C) = n(A) + n(B) + n(C) - n(A⋂B) - n(B⋂C) - n(A⋂C) + n(A⋂B⋂C)
- n(A) = n(A⋃B) + n(A⋂B) - n(B)
- n(B) = n(A⋃B) + n(A⋂B) - n(A)
- n(A - B) = n(A) - n(A⋂B)
- n(A - B) = n(A⋃B) - n(B)
- n(B - A) = n(A⋂B) - n(A)
- n(B - A) = n(B) - n(A⋂B)
- If A⋂B = Φ, then n(A⋃B) = n(A) + n(B)
- If A⋂B = Φ, then A - B = A
- (A')' = A
- A⋃A' = U
- A⋂A' = Φ
- A⋂Φ = Φ
- U⋂A = A
- A⋃Φ = A
- U⋃A = U
- U' or Uc = Φ
- Φ' = U
- n(A') = n(U) - n(A)
Properties in sets
Many properties in the sets. Some important properties are given below.
Symmetric difference
A△B = (A - B)⋃(B - A)
A△B = (A⋃B) - (A⋂B)
A⋂B' = A - A⋂Bn(A⋂B') = n(A) - n(A⋂B)
Similarly,
n(A'⋂B) = n(B) - n(A⋂B)
Idempotent law
A⋃A = A
A⋂A = A
Identity law
A⋃Φ = A
A⋂U = A
Commutative law
A⋃B = B⋃A
A⋂B = B⋂A
Associative law
(A⋃B)⋃C = A⋃(B⋃C)
(A⋂B)⋂C = A⋂(B⋂C)
Distributive law
A⋃(B⋂C) = (A⋃B)⋂(A⋃C)
A⋂(B⋃C) = (A⋂B)⋃(A⋂C)
De morgan's law
(A⋃B)' = A'⋂B'
(A⋂B)' = A'⋃B'
Disjoint sets Properties
n(A⋃B) = n(A) + n(B)
A⋂B = Φ
n(A - B) = n(A)
Don't forget to share with friends and support🙏
Progression || A.P., G.P., H.P.
Average Definition and formulas
Average Questions with solution
Inverse Trigonometric function formulas pdf








Post a Comment
Please do not enter any site link in the comment box 🚫.